超正方體（Tesseract, hypercube）又稱超立方體或正八胞體，在幾何學中四維方體是立方體的四維類比，四維方體之於立方體，就如立方體之於正方形，四維方體是四維凸正多胞體，有8個立方體胞，立方體維數大於3推廣的是超立方體或測度多胞體。

超立方體，又作正八胞體(8-cell,Regular octachoron)，立方體柱(Cubic prism)，4-4邊形柱(4-4 duoprism)，是一個四維空間里的幾何產物

需要說一下「超立方體」的英文應該是Tesseract而不是Hypercube，Hypercube在英文維基百科上是指N維立方體（一維的線段，二維的正方形，三維的立方體……）的總稱

施萊格爾投影

四維方體不易想像，但可以投射至3維或2維空間。在2維平面的投射，把頂點位置調整後，可以了解更多。如此獲得的圖像，不再反映四維方體空間構造，而是反映頂點間的聯繫。

 

對於生活在三維空間的人類來說，四維世界是很神秘的概念。正像生活在二維世界裡的小人（如果存在）很難想像三維世界一樣，我們同樣難於想像四維世界。不過也正像我們可以通過研究三維物體在二維物體上的投影來研究想像三維物體一樣，我們也可以通過四維物體在三維世界中的立體圖形投影來研究四維世界。

 

圖1 所示的是一個立方體在二維世界中的投影。二維小人多多少少可以通過這些投影來想像那個「三 維立方體」的神秘圖形。他們可以數出這個立方體有8個頂點，12條邊，6個面。

 

可以看到圖1的樣子像是一個大正方形套一個小正方形，那我們用一點類比的思維，把一個大立方體「套住」一個小立方體，這就得到一個超正方體的一種三維投影（當然圖2又是它的二維投影）

 

正如圖1的投影中，立方體的六個面也要把最外部的正方形也要算進去，超正方體表面的八個立方體也包括「最外部」的那一個

 

可以知道，超正方體有8個胞（立方體）、24個面（正方形）、32條棱和16個頂點 　　值得說一下的是，在圖2中，投影后一大一小兩個立方體的邊長比正好是3:1，這個是通過計算得到的。

 

 

值得說一下的是，在圖2中，投影后一大一小兩個立方體的邊長比正好是3:1，這個是通過計算得到的。

思維方式
　　如果四維超正方體不太好想像的話，我們換成球試試吧。三維球嘛，無論從哪個方向投影在二維平面上都只是一個半經等同的圓形，這樣我們就很容易想到四維球在三維世界中的投影只不過是一個半徑等同的球了。如果還想要討論得深入一些，不妨試試球穿越問題。比如說一個球穿過一個二維平面，二維小人會發現平面上憑空冒出一個慢慢變大的點，後來眼看著擴張成圓，又慢慢縮小成點，最後突然消失。如果這個令二維小人驚訝不已的事實讓你並不覺得奇怪，那麼以下的情形你定會吃驚不小；在你面前無中生有地出現一個點，擴成球又縮回點，再突然消失。多麼神奇！其 實這只不過是四維球穿越三維世界的情形。

 

這裡講一種思維方式，當你不能夠理解四維的某些描述的時候，試著把自己當作二維人生活在扁平的世界裡看三維(你能夠理解，但是你的描述是受限的)。

 

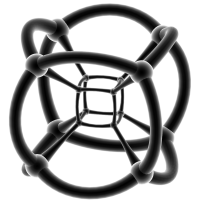
將一個立方體的各個表面膨脹，一段時間後會得到一個球

同樣的方法，將超正方體的表面膨脹，會得到一個「超球」(Hypersphere)

當我們置身於超正方體膨脹成的超球中的時候，我們就會看見右圖的這個情景——此時我們置身在「最外部」的立方體（當然是膨脹了的）面上

 

平行投影

　　上面的兩種其實都屬於透視投影——實際上立方體的平行投影是絕對不會出現一大一小大正方形

 

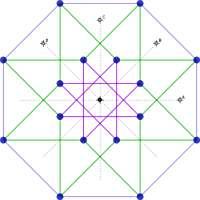
四維超正方體不但可以投影到三維，而且也可以直接投影到二維平面上（是直接，不經過三維），但是由於是投影在二維上，會失真得很厲害。所以只能夠表現一些點與線之間的連接關係 　　右圖是超正方體的二維線架正投影，ABCD分別是四個軸，注意「相鄰」兩根軸的夾角都是45度的。16個頂點坐標分別是(±1,±1,±1,±1)（下文有簡單推導），然後按照給出的一個一個填上去就是的了（方法說上去有點煩，大家可以用幾何畫板畫畫這個投影，其實蠻簡單的）。

大家一定知道把立方體的六個面展開的樣子吧，其中一種展開法如右圖。

 

類比一下，即可得到超正方體的其中一種展開法，如最右圖，其中一個立方體被藏在三維展開圖裡邊了。

 

看上去很奇怪是吧，這八個立方體在我們的世界裡無論怎麼翻轉也不能組成一個超正方體的，它們必須在四維空間里旋轉——這個比方就好比二維小人不會明白那六個正方形怎麼轉才能拼成一個立方體一樣的道理。

 

零維的一個點，包含一個零維元素（點）；一維的一條線段，包含一個一維元素（線段），兩個零維元素；二維的一個正方形，包含一個二維元素（面），四個一維元素；三維的一個正方體，包含 一個三維元素（三維立體），六個二維元素，十二個一維元素，八個零維元素

 

對比下列算式：

(x+2)^0=1

(x+2)^1=x+2

(x+2)^2=x^2+4x+4

(x+2)^3=x^3+6x^2+12x+8

可以歸納出：一個n維立方形(n-cube)所包含的k維元素個數等於(x+2)^n展開式的k次項係數。

(x+2)^4=x^4+8x^3+24x^2+32x+16

可以得出：超正方體有8個立方體（胞），24個面，32條線段，16個點。

這有助於我們印證四維超正方體的構造。

超正方體Tesseract的施萊夫利符號有幾個

{4,3,3}(特指它是正多胞體Tesseract)；

{4,3}x{}（代指Cubic prism）；

{4}x{4}(4-4 duoprism，由兩個正方形絕對垂直得到)；

{4}x{}x{}（代指Square prismatic prism，就是一個正方形柱——通俗的說還是立方體——的柱形）；

{}x{}x{}x{}（代指Line segmentary prismatic prismatic prism，這個……）。

超正方體的頂點坐標可以用類比的方式推導：

正方形的坐標：（±1，±1）

正方體的坐標：（±1，±1，±1）

那麼類比可以得到四維超正方體的頂點：（±1，±1，±1，±1）

哇，這新版詞條是我寫的哈哈

——yaoliding