【百度百科】超正方体_四維幾何學吧

1樓巨大八爪鱼 2011-3-12 10:10

超正方体（Tesseract, hypercube）又称超立方体或正八胞体，在几何学中四维方体是立方体的四维类比，四维方体之于立方体，就如立方体之于正方形，四维方体是四维凸正多胞体，有8个立方体胞，立方体维数大于3推广的是超立方体或测度多胞体。

2樓巨大八爪鱼 2011-3-12 10:11

超立方体，又作正八胞体(8-cell,Regular octachoron)，立方体柱(Cubic prism)，4-4边形柱(4-4 duoprism)，是一个四维空间里的几何产物

需要说一下“超立方体”的英文应该是Tesseract而不是Hypercube，Hypercube在英文维基百科上是指N维立方体（一维的线段，二维的正方形，三维的立方体……）的总称

3樓巨大八爪鱼 2011-3-12 10:14

施莱格尔投影

四维方体不易想象，但可以投射至3维或2维空间。在2维平面的投射，把顶点位置调整后，可以了解更多。如此获得的图像，不再反映四维方体空间构造，而是反映顶点间的联系。

对于生活在三维空间的人类来说，四维世界是很神秘的概念。正像生活在二维世界里的小人（如果存在）很难想象三维世界一样，我们同样难于想象四维世界。不过也正像我们可以通过研究三维物体在二维物体上的投影来研究想象三维物体一样，我们也可以通过四维物体在三维世界中的立体图形投影来研究四维世界。

图1 所示的是一个立方体在二维世界中的投影。二维小人多多少少可以通过这些投影来想象那个“三维立方体”的神秘图形。他们可以数出这个立方体有8个顶点，12条边，6个面。

可以看到图1的样子像是一个大正方形套一个小正方形，那我们用一点类比的思维，把一个大立方体“套住”一个小立方体，这就得到一个超正方体的一种三维投影（当然图2又是它的二维投影）

正如图1的投影中，立方体的六个面也要把最外部的正方形也要算进去，超正方体表面的八个立方体也包括“最外部”的那一个

可以知道，超正方体有8个胞（立方体）、24个面（正方形）、32条棱和16个顶点　　值得说一下的是，在图2中，投影后一大一小两个立方体的边长比正好是3:1，这个是通过计算得到的。

值得说一下的是，在图2中，投影后一大一小两个立方体的边长比正好是3:1，这个是通过计算得到的。

4樓巨大八爪鱼 2011-3-12 10:18

思维方式
　　如果四维超正方体不太好想象的话，我们换成球试试吧。三维球嘛，无论从哪个方向投影在二维平面上都只是一个半经等同的圆形，这样我们就很容易想到四维球在三维世界中的投影只不过是一个半径等同的球了。如果还想要讨论得深入一些，不妨试试球穿越问题。比如说一个球穿过一个二维平面，二维小人会发现平面上凭空冒出一个慢慢变大的点，后来眼看着扩张成圆，又慢慢缩小成点，最后突然消失。如果这个令二维小人惊讶不已的事实让你并不觉得奇怪，那么以下的情形你定会吃惊不小；在你面前无中生有地出现一个点，扩成球又缩回点，再突然消失。多么神奇！其实这只不过是四维球穿越三维世界的情形。

这里讲一种思维方式，当你不能够理解四维的某些描述的时候，试着把自己当作二维人生活在扁平的世界里看三维(你能够理解，但是你的描述是受限的)。

将一个立方体的各个表面膨胀，一段时间后会得到一个球

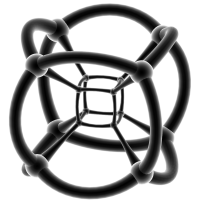
同样的方法，将超正方体的表面膨胀，会得到一个“超球”(Hypersphere)

当我们置身于超正方体膨胀成的超球中的时候，我们就会看见右图的这个情景——此时我们置身在“最外部”的立方体（当然是膨胀了的）面上

平行投影

　　上面的两种其实都属于透视投影——实际上立方体的平行投影是绝对不会出现一大一小大正方形

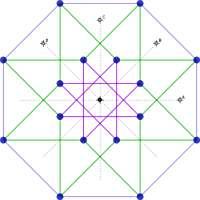
四维超正方体不但可以投影到三维，而且也可以直接投影到二维平面上（是直接，不经过三维），但是由于是投影在二维上，会失真得很厉害。所以只能够表现一些点与线之间的连接关系　　右图是超正方体的二维线架正投影，ABCD分别是四个轴，注意“相邻”两根轴的夹角都是45度的。16个顶点坐标分别是(±1,±1,±1,±1)（下文有简单推导），然后按照给出的一个一个填上去就是的了（方法说上去有点烦，大家可以用几何画板画画这个投影，其实蛮简单的）。