不定积分是微分的逆运算,不是求导的逆运算,所以积分符号后面当然要跟上微分的运算结果(也就是微分式)。例如0,(4+x)dx,7dx等都是微分的运算结果,而8则是求导的运算结果,不是微分的运算结果,所以∫8是没有意义的。注意4+dx不是微分运算的结果,因为没有哪个函数只进行微分运算后能得到4+dx,必须要先微分再进行一次加法运算才能得到。
设p = 4xdx,那么d(2x²)=p,也就是说对2x²进行微分运算后,其运算结果是p。由于不定积分是微分的逆运算,那么∫p肯定就等于2x²。
再看下面的例子:
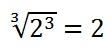
可以看出开方符号里面也有乘方运算。若f(x)=x³,并规定符号√为
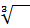
(也就是∛),那么上式就可以写为√f2=2,也可以写为√8f1=2,并且8f1=f2。这个就和∫d(sinx)=sinx,∫cosxdx= sinx,d(sinx)=cosxdx很相似。
若有方程8fx=f(7+3x),那么两边进行√运算:√8fx=√f(7+3x),因为8fx=f(2x)(这个根据√的运算性质可以得到),所以可以得到:2x=7+3x,因此x=-7。这个非常类似于解微分方程。
那么为什么√8有意义,∫8就没有意义了呢?这是因为8可以是乘方运算的结果,但却不可能是微分运算的结果。
我觉得,课本上在讲不定积分的时候压根就不该提到求导。直接说,不定积分是微分的逆运算。因为d(2x³)=6x²dx,所以∫6x²dx = 2x³;因为d(3x²)=3d(x²),所以∫3d(x²)=3x²;因为找不到一个函数使d(?)=6x,所以∫6x无意义。然后说∫6x²dx里面的6x²dx叫做被积表达式,不说6x²叫被积函数。这样的话肯定就没人再问dx是什么了。