|
【资料】正多胞体 |
 初級魔法師 五級 |
正多胞体定义:
它是一个四维空间上的多胞形(Polytope,点、线段、多边形、多面体,以及更高维度的几何物体的总称)
多胞体表面(Facet)由有限个正多面体组成,每个顶点情况相同
专业点说,就是每一个顶点图(Vertex figure)都是正多面体
简单而言,就是正多胞体中每一条棱外一点旋转一圈,都会穿过相等数目的面(或体)
|
 初級魔法師 五級 |
一个关于正多面体二面角的列表:  考虑到正多胞体里正多面体必须是有限个的,因此一条棱上的几个面的相邻夹角总和(棱上所有多面体的二面角之和)必须小于360度 60°≤70.53°<72°,可知由正四面体组成的正多胞体有三个,分别是每条棱上有三个、四个和五个正四面体,分别对应施莱夫利符号{3,3,3}、{3,3,4}、{3,3,5} 90°≤90°<120°,可知由立方体组成的正多胞体有一个,它的每条棱上有三个立方体,对应施莱夫利符号{4,3,3} 90°≤109.47°<120°,可知由正八面体组成的正多胞体有一个,它的每条棱上有三个正八面体,对应施莱夫利符号{3,4,3} 90°≤116.57°<120°,可知由正十二面体组成的正多胞体有一个,它的每条棱上有三个正十二面体,对应施莱夫利符号{5,3,3} 120°≤138.19°,可知不存在由正十二面体组成的正多胞体 综上可得正多胞体一共有6个:{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5} |
 初級魔法師 五級 |
Pentachoron 正五胞体(5-cell),又作正四面体锥(hyperpyramid),4-单形(4-simplex) 其施莱夫利符号是{3,3,3},顶点图(Vertex figure)是正四面体,在正五胞体中每条棱上有三个正四面体 一般而言,它是正四面体的四维类比 下图是它的施莱格尔(透视)三维投影图,下同: 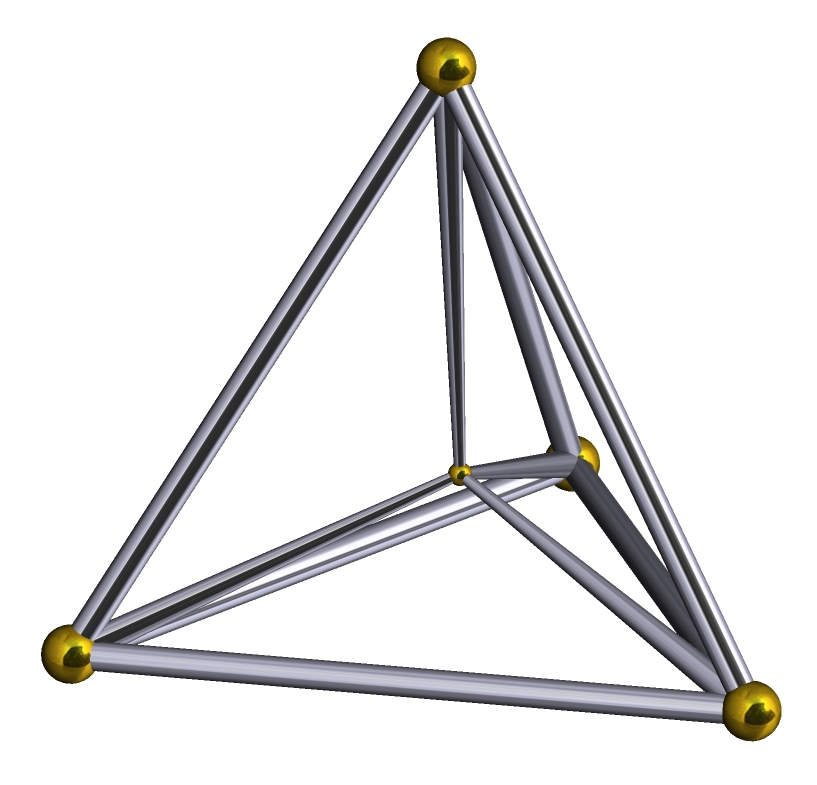 及球极投影图,下同: 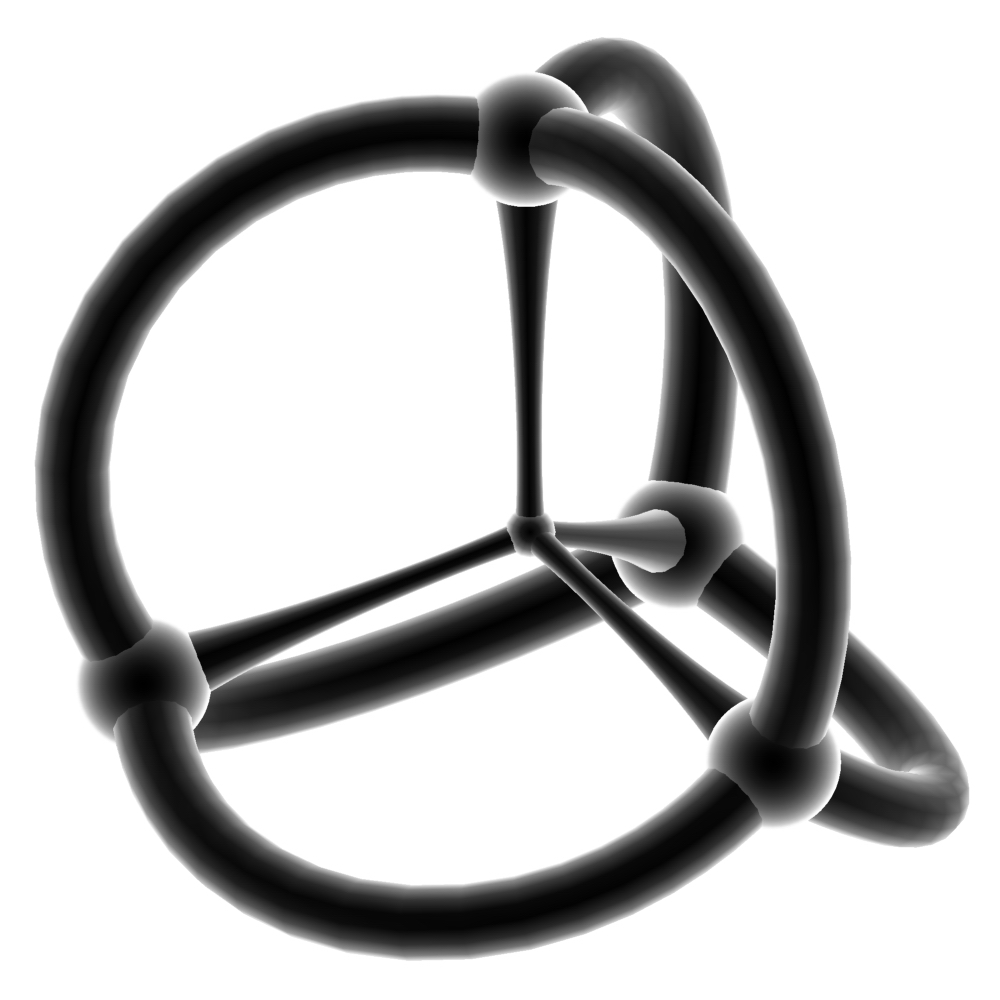 正多胞体里的多面体数(还有顶点数、棱数、面数)都是根据这两个图“数”出来的 正四面体胞:5,正三角形面:10,棱数:10,顶点数:5 平行投影图(二次平行投影,由四维通过平行投影至三维,再由三维平行投影至二维) 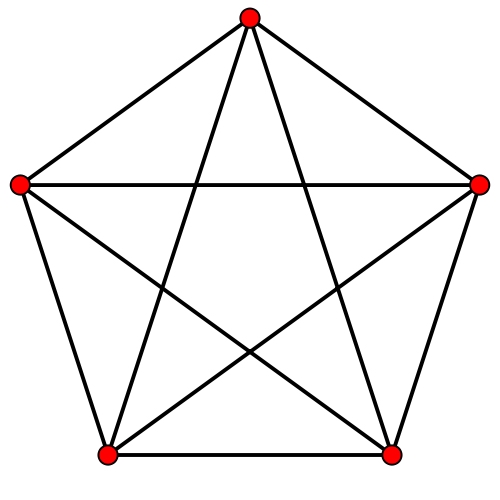 所有正多胞体中最简单的了,作一个正五边形,让五个点两两连线即可 一个正五胞体的正面图:  一个正五胞体的旋转图:  |
 初級魔法師 五級 |
补充:正五胞体带投影面的球极投影:  Tesseract 把一个正方形向第三方向(向上)推移就得到一个立方体,同样把一个立方体向第四方向推移,就会得到一个超立方体 超立方体,又作正八胞体(8-cell,Regular octachoron),立方体柱(Cubic prism),4-4边形柱(4-4 duoprism) 另:“超立方体”的英文是Tesseract而不是Hypercube,Hypercube在wiki上是指N维立方体(一维的线段,二维的正方形,三维的立方体……)的总称 Tesseract,立方体胞:8,正方形面:24,棱数:32,顶点数:16 它
的施莱夫利符号有几个{4,3,3}(特指它是正多胞体Tesseract);{4,3}x{}(代指Cubic prism);{4}x{4}(4-4
duoprism);{4}x{}x{}(代指Square prismatic prism);{}x{}x{}x{}(代指Line
segmentary prismatic prismatic prism,这个……)。顶点图是正四面体,在超立方体中每条棱上有三个立方体 不用说,它就是立方体的四维类比 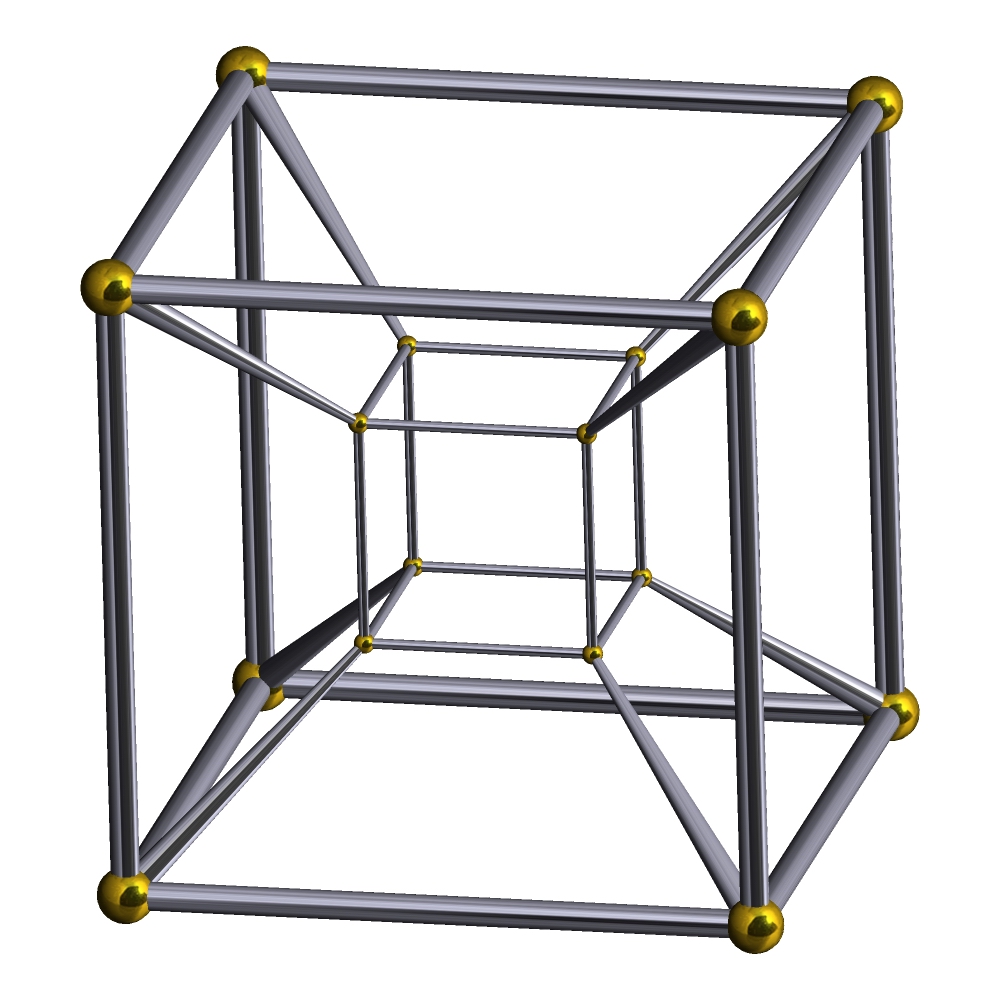 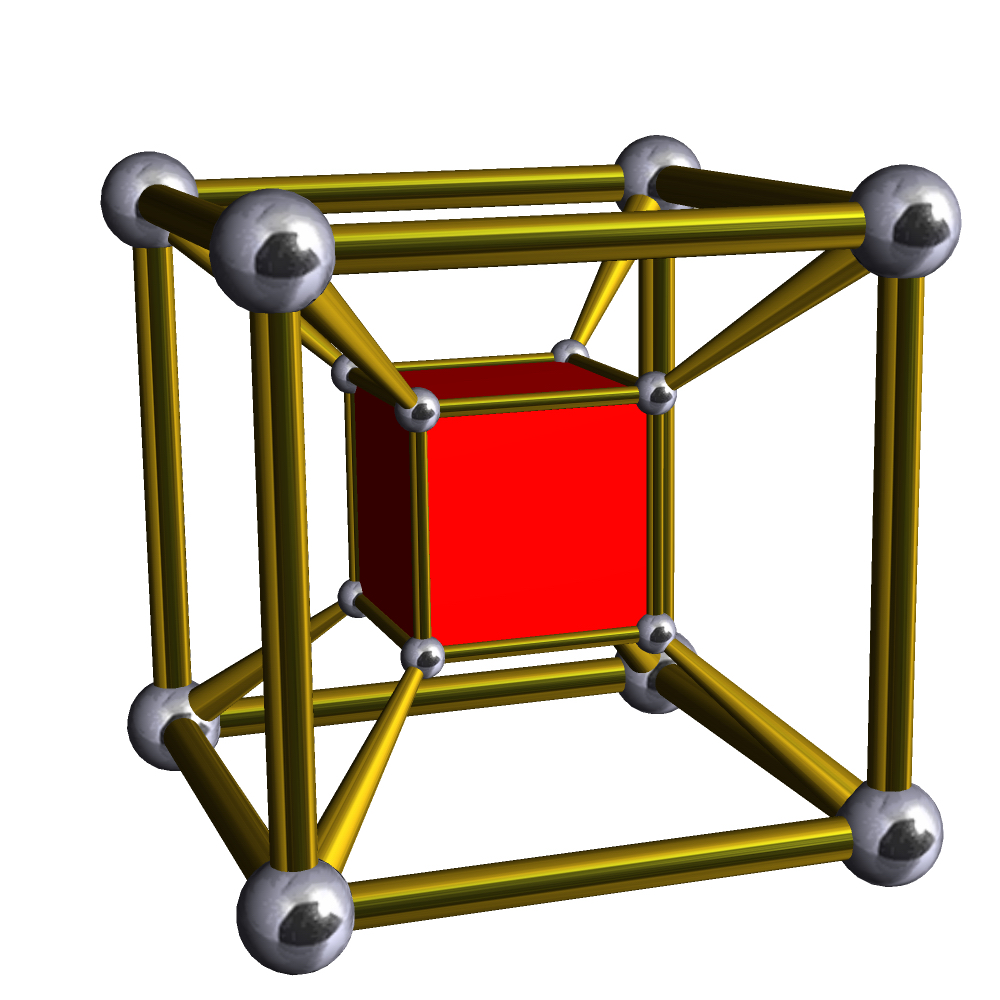 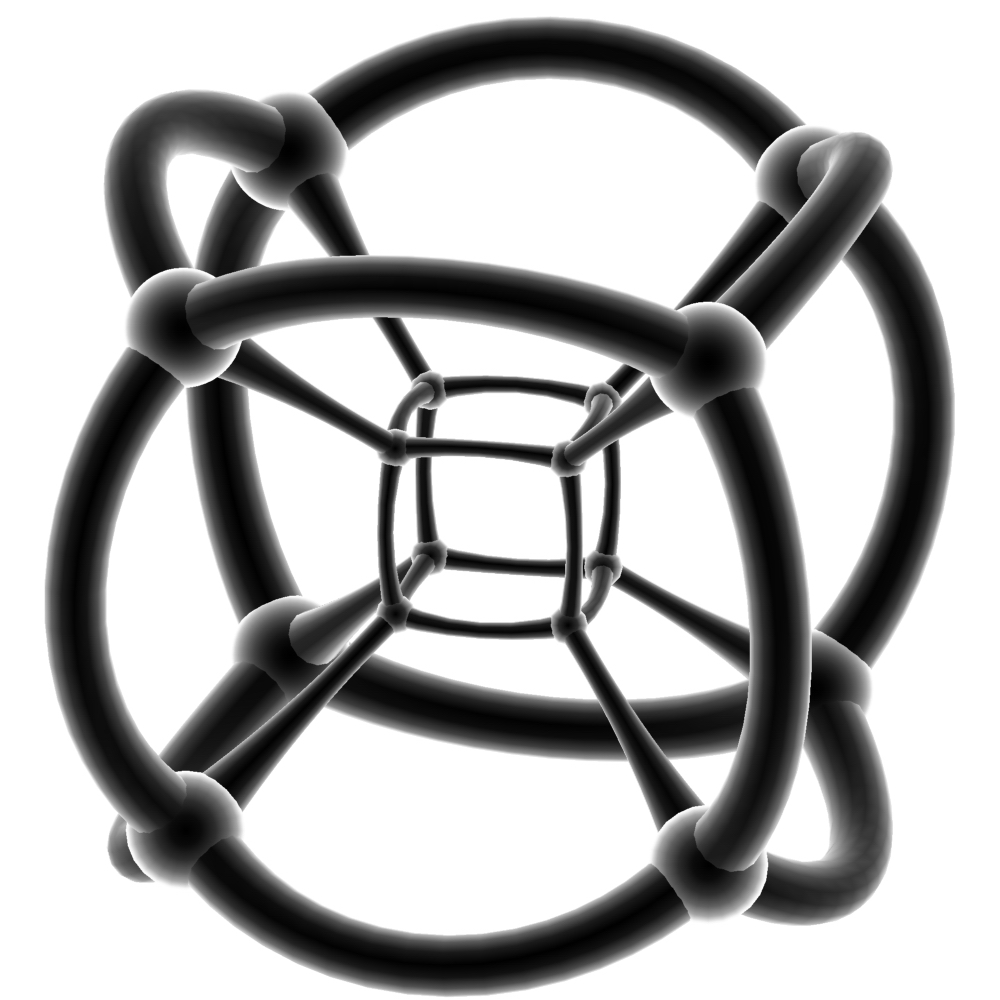 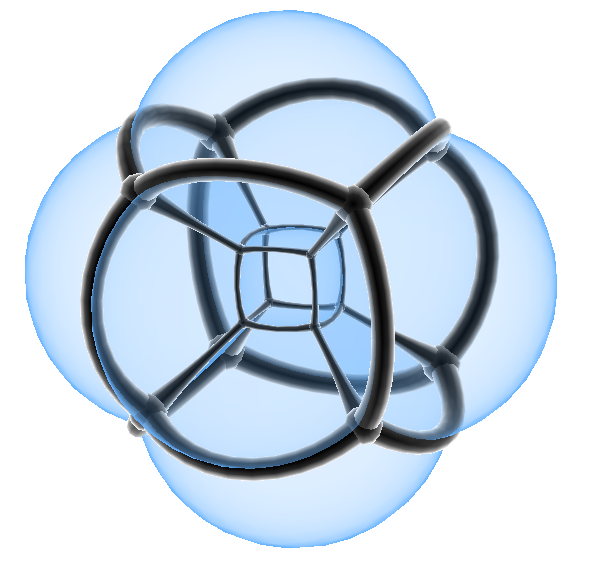 像立方体6个面展开一样,超立方体的展开图:  平行投影: 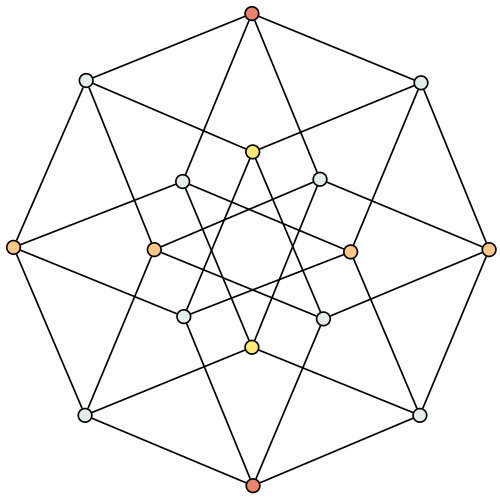 在平面上画四根轴,其中相邻轴的夹角为45度(每根轴的单位长度相等),再在平面上标出超立方体的十六个顶点(±0.5,±0.5,±0.5,±0.5),然后连线(表达很繁琐,过程很简单) 超立方体的旋转图wiki上有很多,个人觉得下面这个最好  |
 初級魔法師 五級 |
我现在才发现当年写这种东西的时候表达能力有多么糟糕
不说了,照发
Hexadecachoron 将一个正方形不相邻的两点连线,得到一个正二边形(Demisquare);将一个立方体两两不相邻的四个点沿各自的面连线(Demicube),得到一个正四面体;同样地,将一个超立方体两两不相邻的八个点沿各自的面连线后,正好会得到它的对偶——正16胞体 它穿过我们空间的时候我们会看见一个又零开始匀速增大的正八面体,一段时间后又以相同的速度缩小,直到消失,这便得到一个正16胞体 正十六胞体(16-cell),又作正四面体反棱柱(Tetrahedron antiprism)、 又作Tetracross(四维交叉多胞形(?),日文“4-正轴体”,没有中文翻译)、 又作4-orthoplex(也没有中文翻译,一个N维的orthoplex和cross都指代同一个多胞体,但意义不同)、 又作Demitesseract(照样没有中文翻译,指代第一段超立方体上连线得到的东东,暂时称为半截超立方体) 16-cell,正四面体胞:16,正三角形面:32,棱数:24,顶点数:8(因为是超立方体的对偶,所以它的数据刚好是反过来的) 它的施莱夫利符号也有几个,{3,3,4}(特指它是正多胞体16-cell);  (特指它是orthoplex,代指Demitesseract);h{4,3,3}(alternated[*] tesseract)等等 其顶点图是正八面体,正16胞体每条棱上有4个正四面体 16-
cell可以通过两种类比方法得到,一种是正八面体的四维类比(正八面体是立方体对偶,顶点为(±1,0,0)
的全排列;而16-cell是超立方体对偶,顶点为(±1,0,0,0)
的全排列),另一种是正四面体的四维类比(上面第一段,正四面体是半截立方体,这不是一个正多胞形的类比方法) 另外,由于正16胞体的二胞夹角为2arctan√3=120°=360°÷3,因此单用正16胞体可以组成一个四维堆砌(相当于二维的均匀镶嵌tiling、三维的均匀堆砌honeycomb)施莱夫利符号{3,3,4,3},每个二维的面上有3个正16胞体 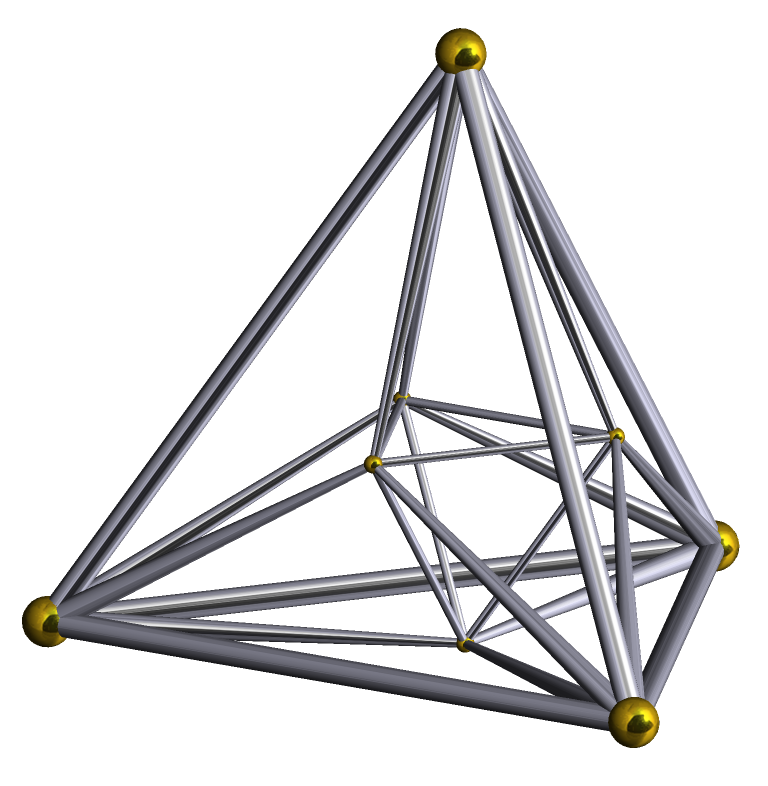   平行投影 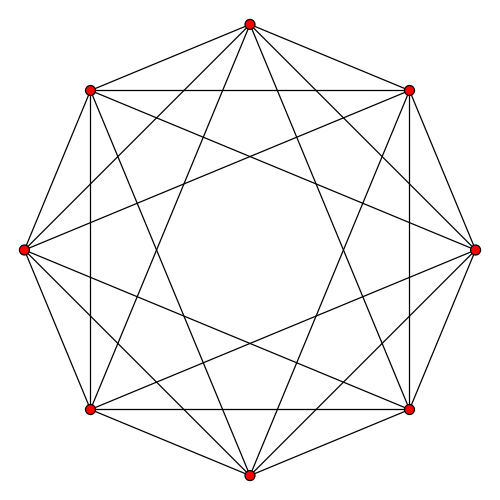 同超立方体一样的方法,画四条轴,标上 (±1,0,0,0)、(0,±1,0,0) 、(0,0,±1,0) 、(0,0,0,±1)八个顶点在连线(作法比超立方体简单多了) 最后是旋转图  |
 初級魔法師 五級 |
回复:5楼 那个没显示出来的小图像是: 
|
 初級魔法師 五級 |
Icositetrachoron 正二十四胞体(24-cell),有时又作复正八面体(octahedral complex),是唯一一个没有三位类比的正多胞体 24-cell,正八面体胞:24,正三角形面:96,棱数:96,顶点数:24(注意到胞数和顶点数,面数和棱数也相等——与正五胞体一样,它也是自身对偶的) 它的施莱夫利符号也有几个,{3,4,3}(特指它是正多胞体24-cell);  (特指它由16-cell截角得到,代指Rectified 16-cell);  (特指它由Demitesseract截角得到,代指Rectified demitesseract——这个东西要涉及Coxeter–Dynkin diagram的,看的懂的求陪同) 其顶点图是立方体,正24胞体每条棱上有3个正八面体 一般而言正方形是24-cell的二维类比,根据它们的施莱夫利符号推算(略)知道,一定意义上它是截半立方体(半正多面体)或菱形十二面体(卡塔兰立体,半正多面体的对偶) 另外,由于正24胞体的二胞夹角也是120°(推导过程不详),因此单用正24胞体也可以组成一个四维堆砌,施莱夫利符号{3,4,3,3},是{3,3,4,3}。每个二维的面上有3个正24胞体 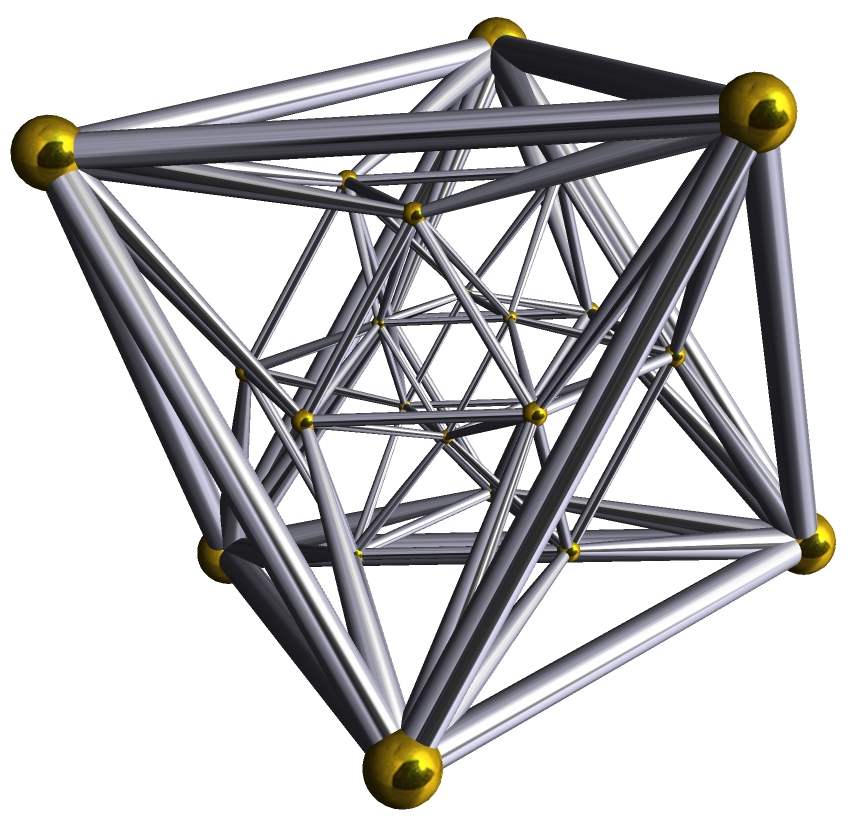  (带投影面)  平行投影(作法不详): 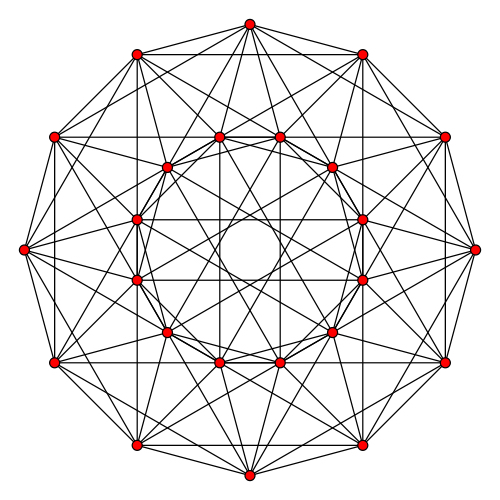 一种没有线条重合的二维投影(非正多边形外框) 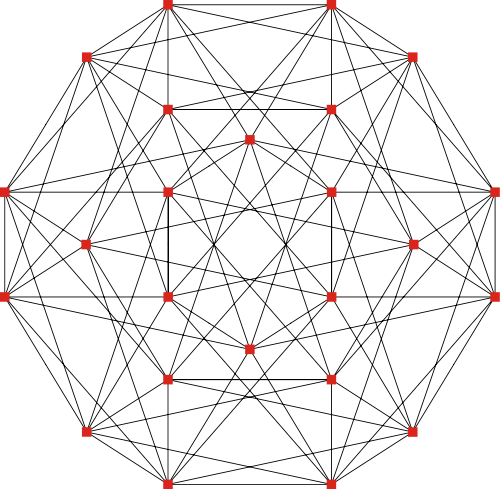 旋转图:  一个24-cell穿过三维空间(太快了,我也没看懂)  补充:分层结构 正如正二十面体一样,表面越复杂的立体分层越明显,以正二十面体的一个面(准确地说是把它的表面都膨胀成球后的一个面上)为极点,将纬度相同的几个面记作同一层,那么正二十面体可分作1-3-6-6-3-1六层(有兴趣的筒子可以拿个正二十面体模型玩玩)。
同样地,正二十四胞体也可以这样分,共五层。不过纬度已经不再指一根线了,而是指四维球表面上的一个“纬面”了 1 cell 相当于北极点 8 cells 约莫北纬面60°处 6 cells 赤道面
8 cells 约莫南纬面60°处
1 cell 相当于南极点 |
 初級魔法師 五級 |
Hecatonicosachoron (最复杂,也是最解说不能的两个来了) 正一百二十胞体(120-cell),又作复正十二面体(Dodecaplex=Dodecahedral complex),超正十二面体(Hyperdodecahedron) 120-cell,正十二面体胞:120,正五边形面:720,棱数:1200,顶点数:600 其施莱夫利符号是{5,3,3},顶点图是正四面体,在正120胞体中每条棱上有三个正十二面体 一般而言,它是正十二面体的四维类比 另
外,由于正120胞体和正600胞体的二胞夹角太大(推导过程不详,我只知道大于120°),因此它们是没办法向更高维度继续类比的,正120胞体的五维
类比是一个坐落在四维的双曲堆砌(Hyperbolic honeycomb in 4 dimension),每个面上有三个正120胞体 再另外,根据120-cell的600个顶点重新连线“连面”可以得到十个星形正多胞体的其中一个(Great grand stellated 120-cell) 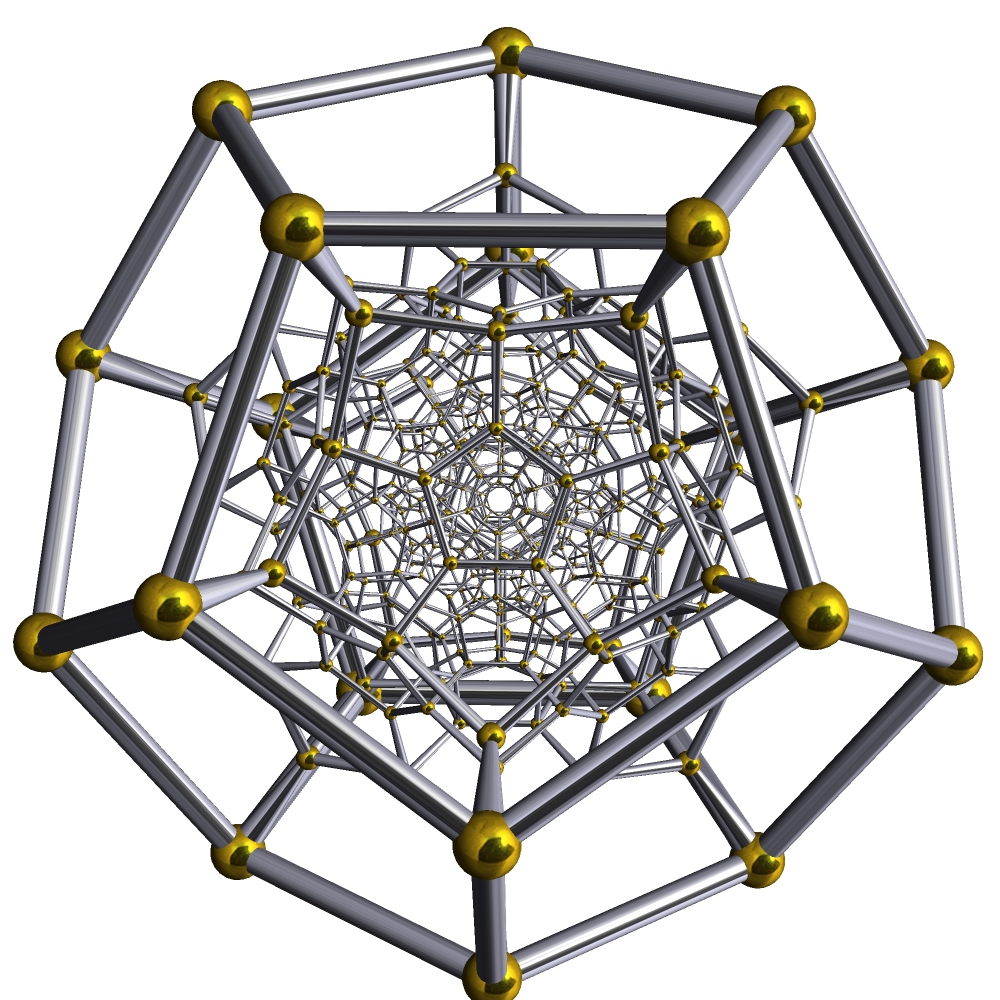 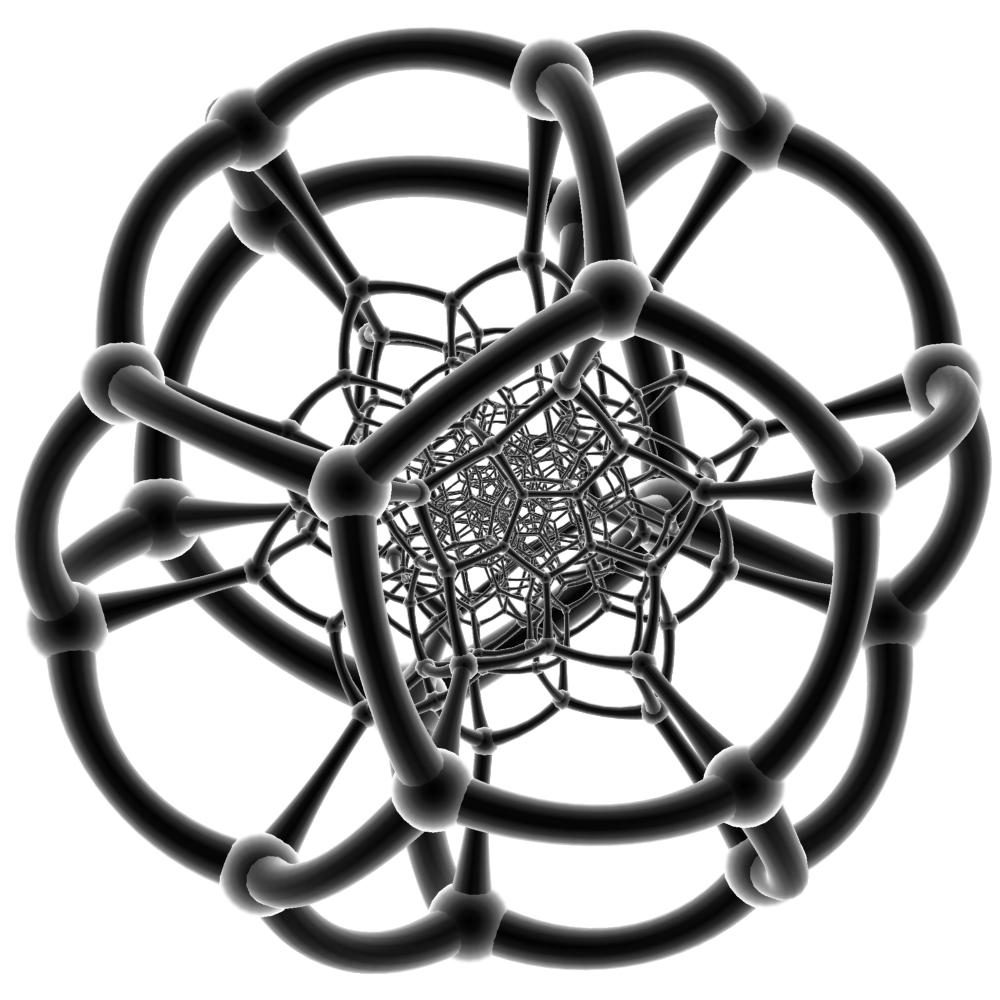 (带投影面)  平面投影(作法:小的连中等数学都没学完,你问我我问谁)(不过话说回来,这种圆盘结构倒挺美妙的): 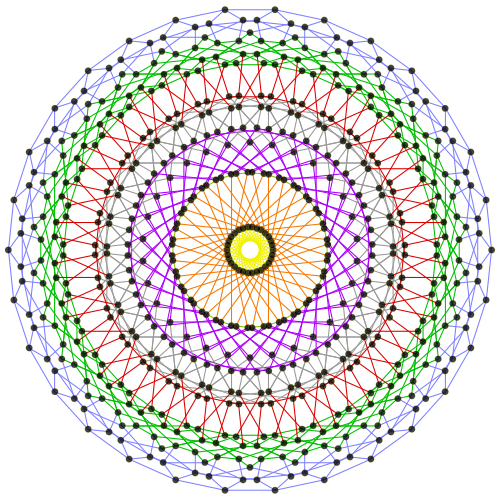 补充:
分层结构,这点在复杂120-cell和600-cell上体现的很明显
这里我照抄维基百科的,不改纬度数了,里面的纬度数都是以北极为0度南极为180度的 1 cell 0°
12 cells 36° 20 cells 60° 12 cells 72° 30 cells 90°
12 cells 108°
20 cells 120° 12 cells 144° 1 cell 180°
拿出其中几个正十二面体表面来看的双环  120-cell的二胞角是144°,求法http://tieba.baidu.com/f?kz=1046741707
最后是旋转图,文件很大,要小心  竟然有内部结构的旋转图  |
 初級魔法師 五級 |
Hexacosichoron 正六百胞体(600-cell),又作复正四面体(Tetraplex=Tetrahedral complex),超正二十面体(Hyper-icosahedron) 600-cell,正四面体胞:600,正三角形面:1200,棱数:720,顶点数:120 正600胞体与正120胞体互为对偶,其施莱夫利符号是{3,3,5},顶点图是正二十面体,在600-cell中每条棱上有五个正四面体 一般而言,它是正二十面体的四维类比 另外,正600胞体的五维类比也是四维的双曲堆砌,施莱夫利符号是{3,3,3,5},与正120胞体的五维类比{5,3,3,3}对偶,它每个面上有五个正五胞体 再另外,根据600-cell的顶点重新连线“连面”可以得到十个星形正多胞体的另外九个(见下一楼) 这
是一个vertex-centered的施莱格尔投影,就是说这个家伙看600-cell眼睛是正对着一个顶点,而不是向前几幅图那样正对着一个多面体胞
的——其实这个vertex-centered投影如果放在球极投影上这个家伙看着的顶点就该处于无限远了,而在这里这个顶点则很不厚道地放在三维投影的
中心 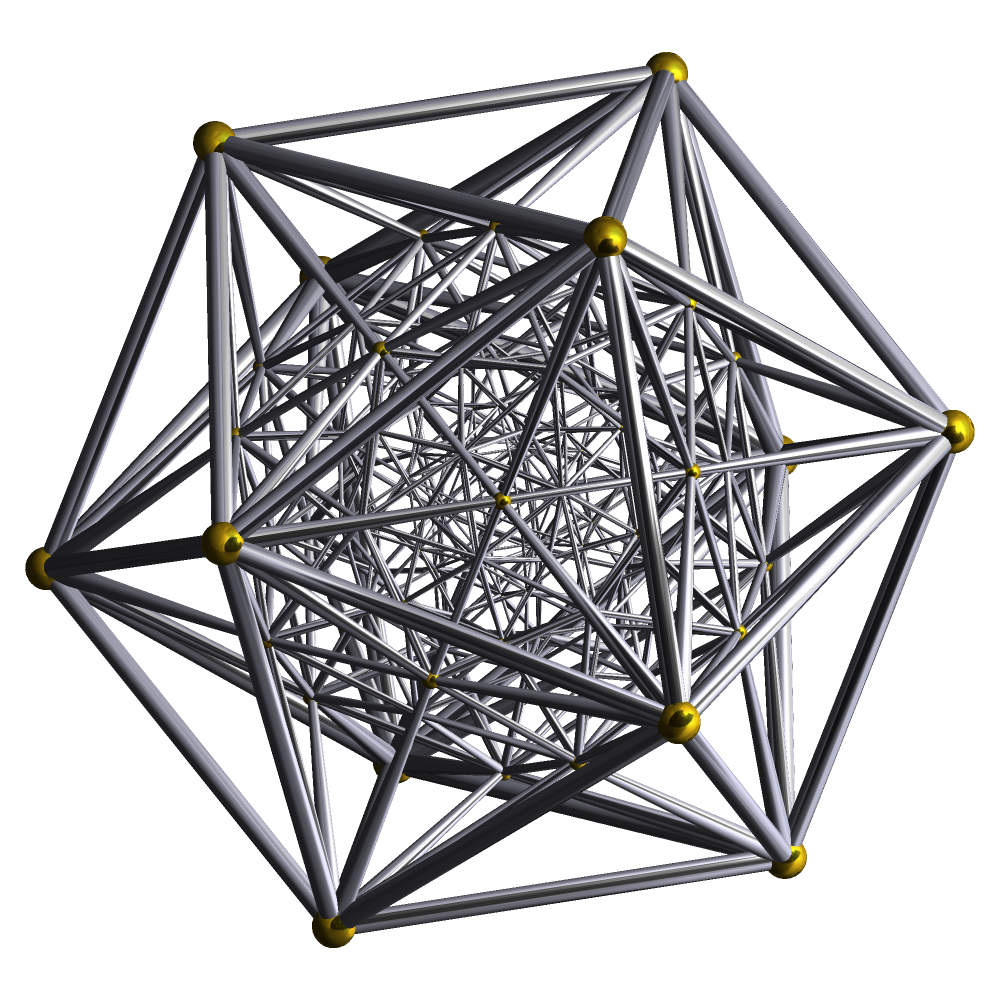  (带投影面) 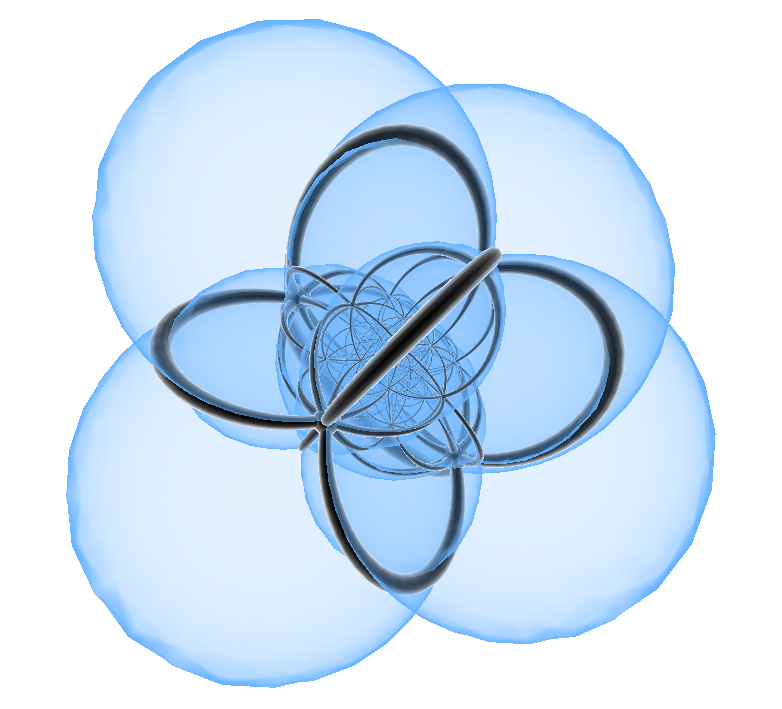 二维线架,做法同上一楼 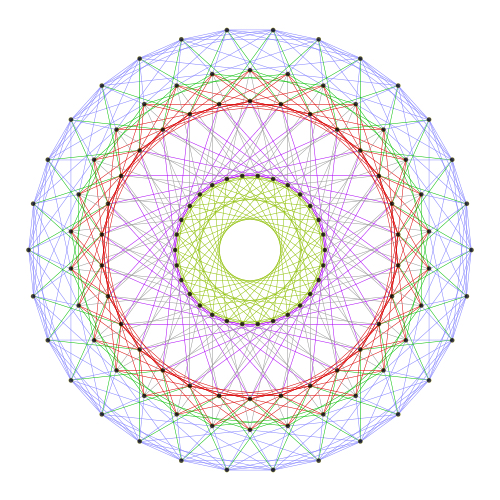 |
 初級魔法師 五級 |
补充
分层结构
600-cell的分层略显犀利了,有31层!
依次是1-4-12-24-12-4-24-24-32-24-12-24-28-24-24-54-24-24-28-24-12-24-32-24-24-4-12-24-12-4-1
分层见http://davidf.faricy.net/polyhedra/Polytopes.html
最后是旋转图,也很大,小心!  |
|
118.117.73.*
|
本文原作者:yaoliding
|
|
183.39.231.*
|
好图,就是分辨率有点低了  |
|
60.182.177.*
|
好像肥皂泡……
|
 一派護法 十九級 |
不过现在英文维基百科上已经有所有正多胞体的展开图了
|
 見習魔法師 二級 |
想到了神经元之间的连接和电路元件之间的连接,电路板作为二维平面所呈现的那种弯曲复杂的点与线之间的结构,在三维空间中可以得到很简洁的体现。 同样的,人脑中神经元之间复杂的连接,在更高维空间中也能以一种更为简洁的形式体现。 |
 一派護法 十九級 |
16樓
發表于: 2015-1-9 23:08

正六百胞體在三維空間的投影十分複雜,但在四維空間中的結構卻十分簡單,僅僅是有表面而已,內部是空心的。
同樣超球在三維空間中的投影,特別是旋轉圖,讓人眼花繚亂。但四維空間中卻是一個極簡單的物體。
|