|
【转载】Fundamental convex & non-convex uniform po |
 初級魔法師 五級 |
写这个估计没人懂的了,我自娱自乐好了 顺便BS一下百度相册,最长边最多只有1600像素,干脆用网易好了 再BS一下,bmp图居然不能点击看大图 一个我在英文wiki上自己改的Polytope的表格,因为几乎全部名称都用英文全名所以被几个老外批太复杂了(大图点击)  |
 初級魔法師 五級 |
完整标题是:Fundamental convex & non-convex uniform polytopes
|
 初級魔法師 五級 |
负一维,拓扑学的最低维度,也是一切多胞形的最终基础, 负一维其实是空空如也的,连自由度都是负数,不可能容纳什么东西 但是每一个多胞形都有且仅有这一个负一维的东西(一般用空集φ表示) 其实下图什么也没有(点击大图)  |
 初級魔法師 五級 |
零维,几何学的最低维度 比起负一维,零维至少有了实物 一个点就是零维,它的自由度为零,当然一个零维空间只能容纳一个点,可以说每个点都是“全等”的,因为一个点的大小必定为“1”(没有单位) 当然点也是多胞形的基础,每个多胞形都有它(那个φ除外),和φ不同,多胞形里的点不止一个 下图表示的就是一个点,当然实际上这个“点”是个二维的圈圈,图片嘛,所有的东西不管高维低维都只展现它的二维投影(点击大图)  |
 初級魔法師 五級 |
一维,有了大小的比较 一条直线就是一个一维空间,有一个自由度,一根线段只能向一个方向(左右)运动 直线延伸到无穷,因此一维有了无穷的概念 一维物体有了大小(长短)之分,也就是说一维物体不完全是全等了,但还是相似的,不是每个多胞形都有一根相同长度的线段,但是一个单位正多胞形与半正多多胞形都拥有一个单位长度的线段(除了零维负一维正多胞形) 和零维负一维一样,一根线段必定是一个“正”的多胞形 下图表示一根线段(点击大图) 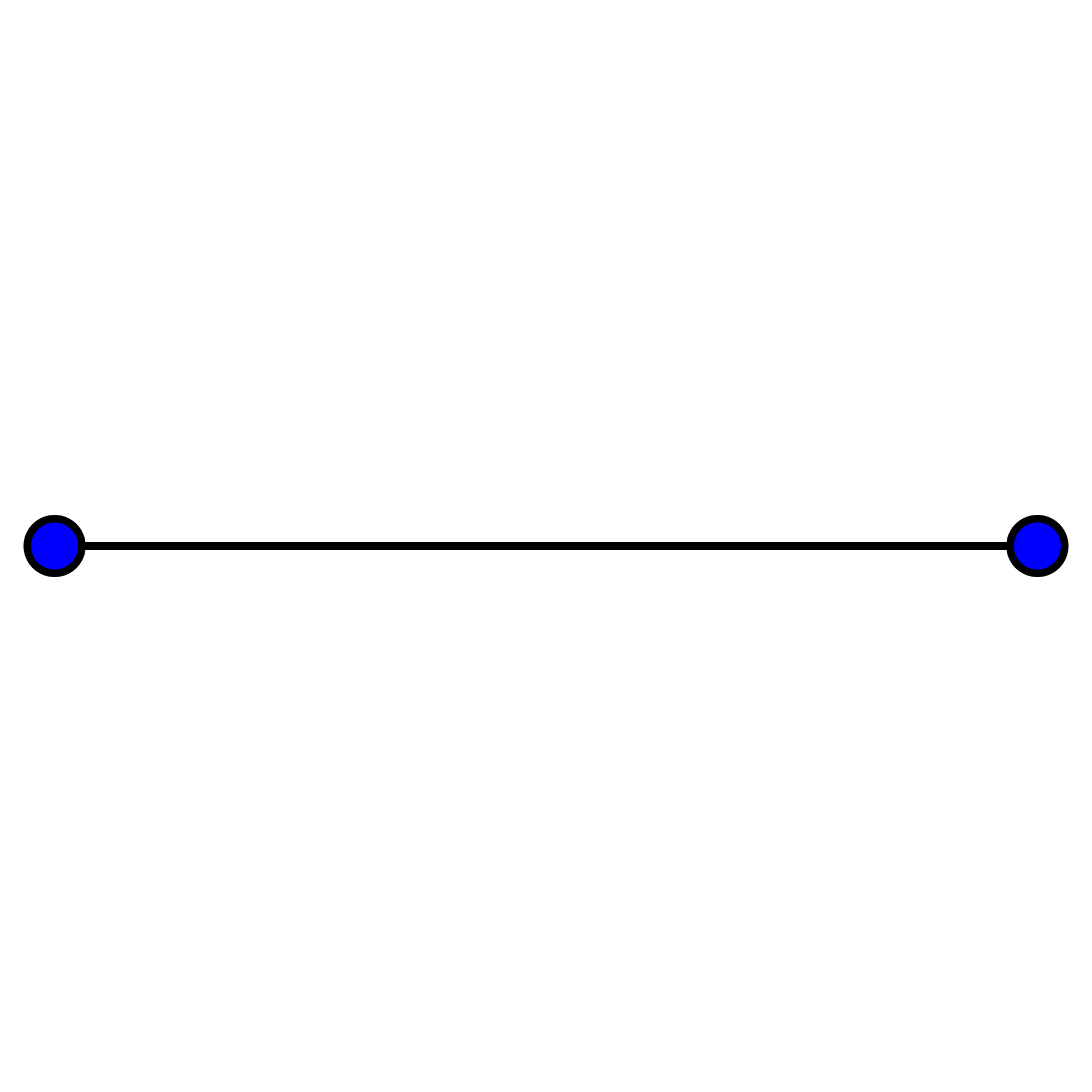 |
 初級魔法師 五級 |
二维,有了真正的方向性
一个平面就是一个二维空间,有两个自由度,一个二维物体不仅仅可以向两个垂直方向运动(前后、左右),还可以向左前、右后这些方向运动,可以说具有了真正的方向性
在二维上可以画一个球面一维空间(圆)
平面几何是从小学一直学到中学的了,可以知道,二维有了垂直、平行(包括严格定义过的相似和全等)还有角度等等这些从未有过的定义
二维的多胞形——多边形,不会完全相似或全等了,大部分的多边形也不再是“正”的多边形了,但是作为二维中的正多胞形——正多边形有无数个(星形也是),比任何维度都要多,其中还有两个拓扑多边形:正一边形(内角公式在这里失效)和正二边形(实际内角为0)
另外二维还有一个一维的欧式正镶嵌(就是一个可以嵌在N-1维空间里的N维的东西)——正无穷边形(Apeirogon),内角为180度,正好可以填满一个平坦一维空间(直线)
二维里也有了顶点图的概念,当然一个多边形的顶点图充其量就是一条线段,有长短之分而已——其中Apeirogon的顶点是在它的顶点图里面的
最后是在Coxeter群里面,二维是多胞形群开始形成(应该说是开始有作用了吧,线段就一种,也看不清它去到二维会变成什么),A群(正三角形)BC群(正方形)G群(正六边形,不知道G群应不应该算进去)H群(正五边形)出现
|
 初級魔法師 五級 |
部分正多边形(点击大图) A2、E2(?)、I3 Triangle  BC2、F2(?)、I4 Kvadrato(Square的世界语)  H2、I5 Pentagon 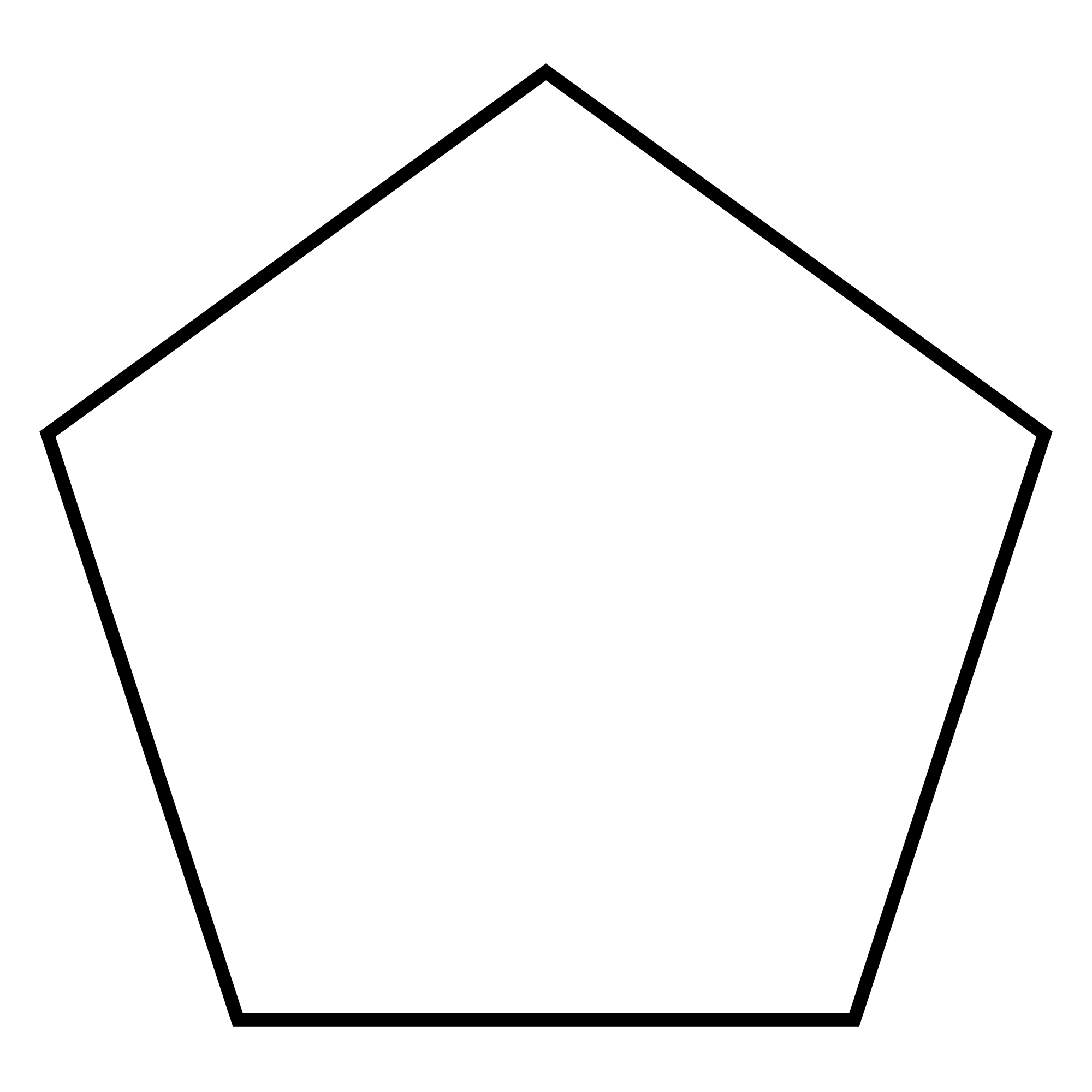 G2、I6 Hexagon 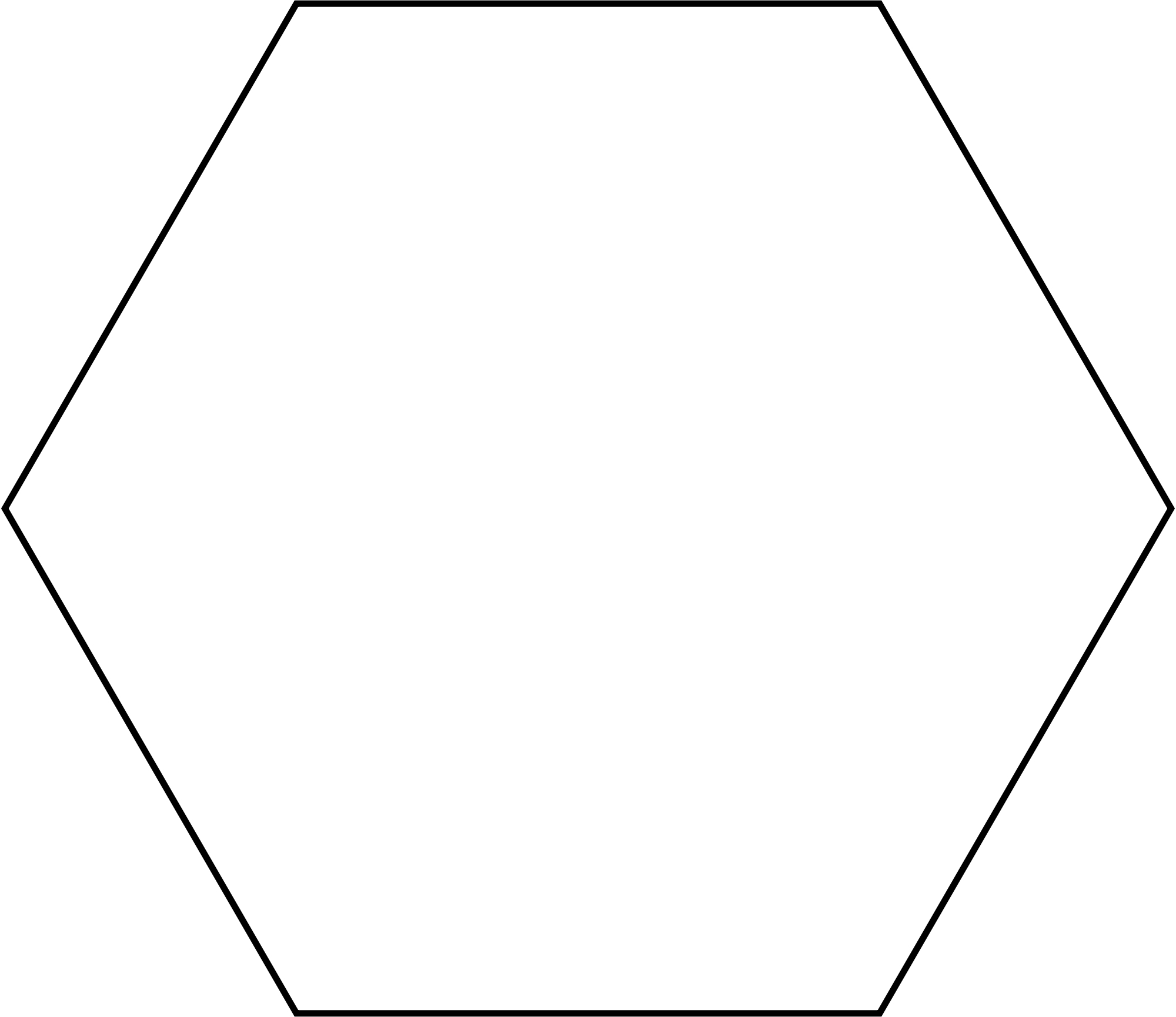 I群是正多边形群。 I群的一个元素In(n是任意正整数)代表正n边形(群论我还没学过,略懂) |
 初級魔法師 五級 |
三维,我们的世界
我们用来生活的空间是三维,这是个不争的事实,可以说三维有很多特殊的地方——当然很大程度上是因为“我们”就存在于此。
就我们的运动而言,我们的身体可以向三个垂直方向运动:上下、左右、前后。即是说,我们的世界具有三个自由度。
二
维中能作一个一维的黎曼空间(圆),在三维就得到一个二维的球面。但除此之外,在平坦三维空间中又可以新作另一种二维曲面:双曲面。作为罗氏空间的最基本
的空间,双曲面就远比黎曼空间球面复杂很多,作为三维生物的我们对双曲面的了解程度远没有对球面的多。(考虑到多胞形一般都是用构成表面的角度去观察,所
以谈论一个维数时会讲到低一维的空间)
相比二维,三维中点线面的关系变更丰富了。在三维,两条直线可以既不平行也不相交;同时旋转变得有向,于是又有了(旋转)轴的概念。等等。
虽然三维比二维新增的东西远没有二维比一维新增的多,但几何学里的复杂程度却是程指数增长的。于是乎学了一个义务教育的平面几何,直到高中才见到立几的身影——毕竟咱们人类对立体几何的研究多少还是有很大的局限性的
说会三维的多胞形——多面体,比起二维“正”的多面体当然是少无数倍了,只有五个,另外星形正多面体有四个。
有少也有多,三维里所谓的“拓扑正多面体”变为无数个了。欧式正镶嵌(所谓的平面正镶嵌)也变成了三个,同时产生了置于罗氏空间的双曲正镶嵌无数个
三维中有了“体”的概念,并沿用至高维,多面体上的顶点图意义也自然得到强化。多边形的还只是雏形,毕竟二维图形的顶点图都是线段,只有长度,也看不出的所以然。多面体的顶点图会因为各自的属性分类的不同会有很大的差异。
在Coxeter群里面,三维是多胞形群开始发展的维度,B群(正八面体)和C群(立方体)分开,D群从拓扑多边形(D2,正二边形)变成真正意义的多面体(D3,正四面体),E群原则上出现(正三棱柱)了。
|
 初級魔法師 五級 |
考克斯特群的基本多面体(含正多面体)(点击大图) A3、D3 Tetrahedron 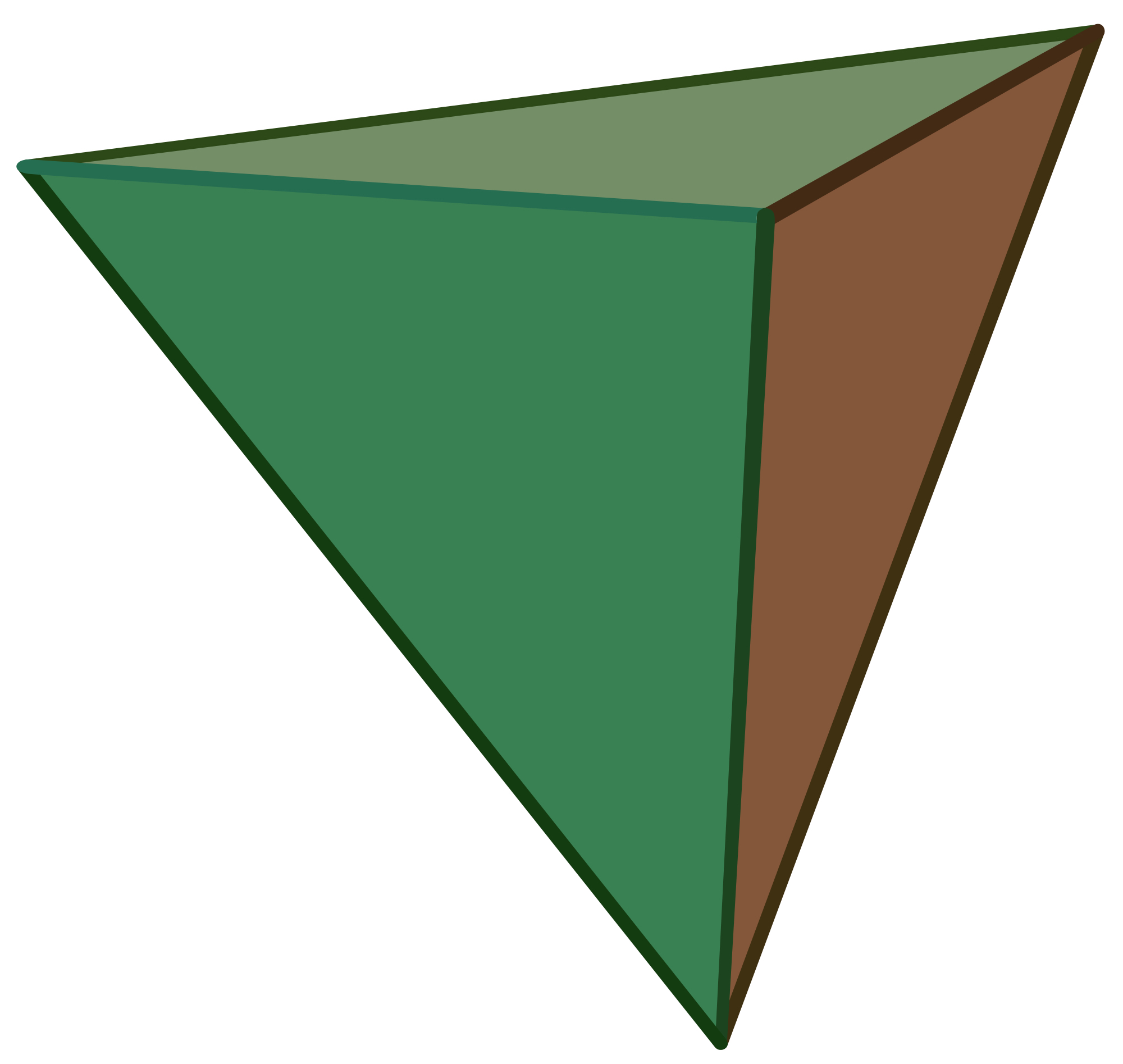 C3 Cube  B3 Octahedron  H3 Dodecahedron  H3 Icosahedron  E3 Trigonal Hosohedron 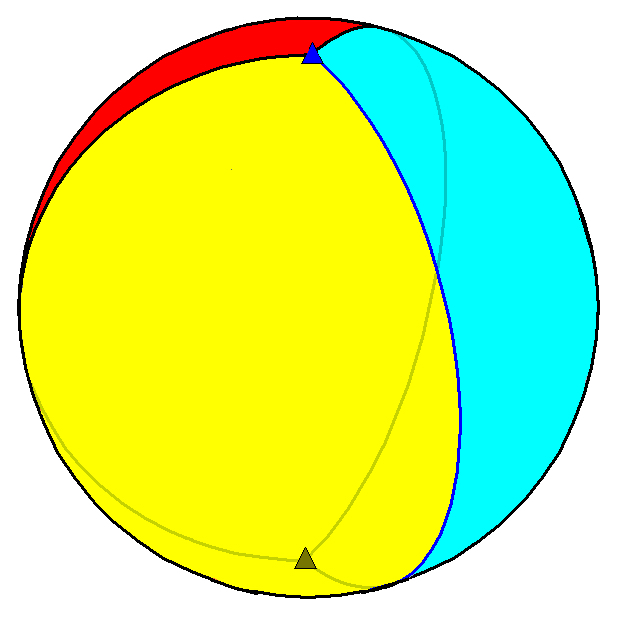 E3 Trigonal Dihedron 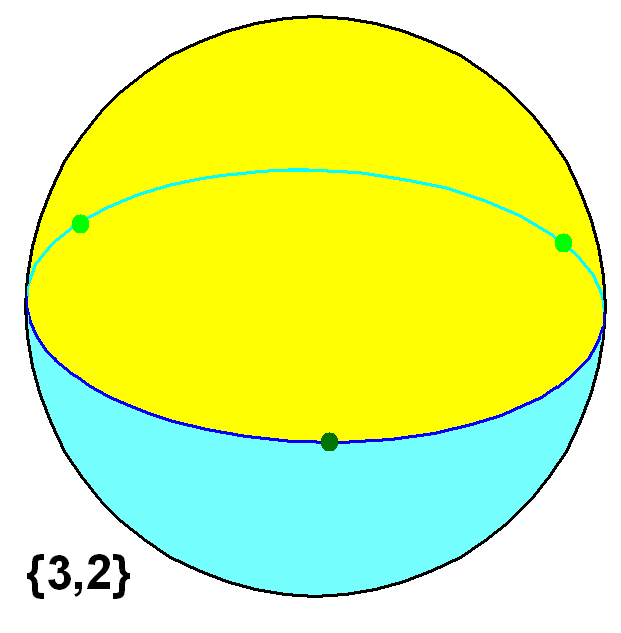 E3 Triangular Prism 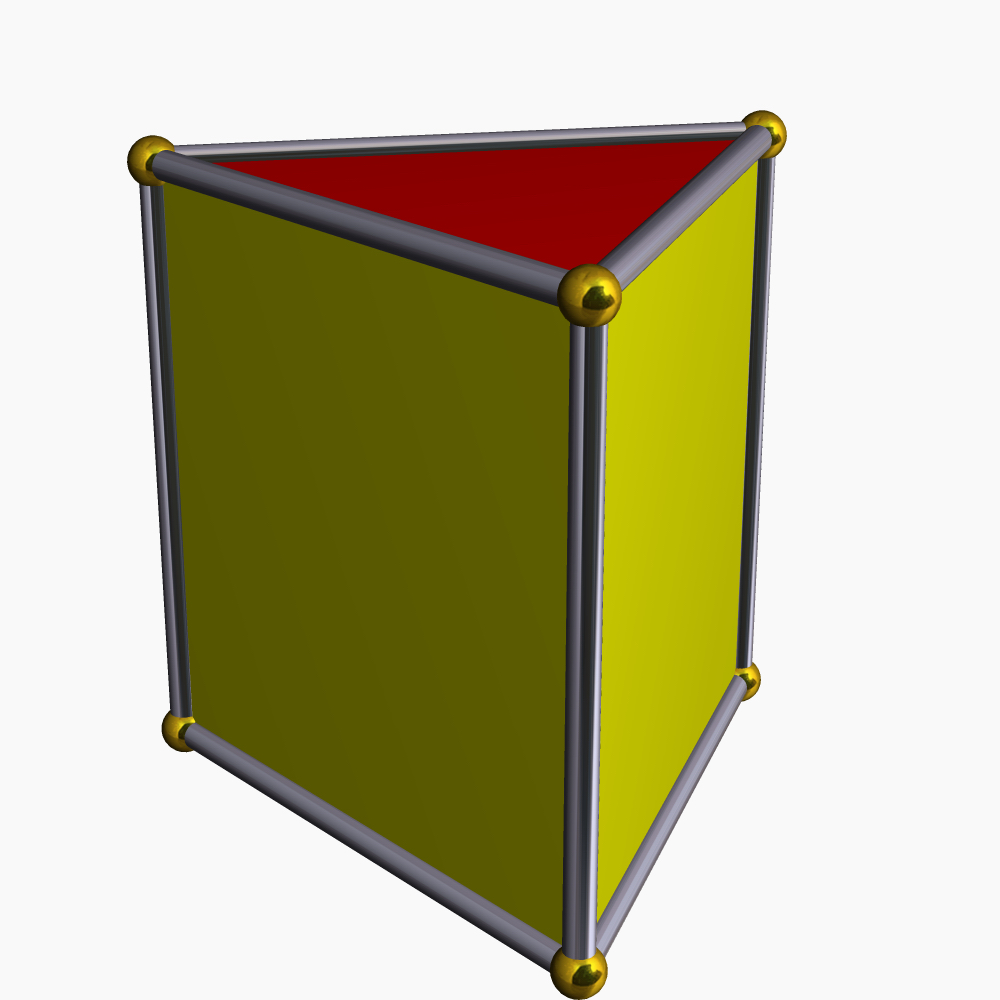 F3(?) Cuboctahedron 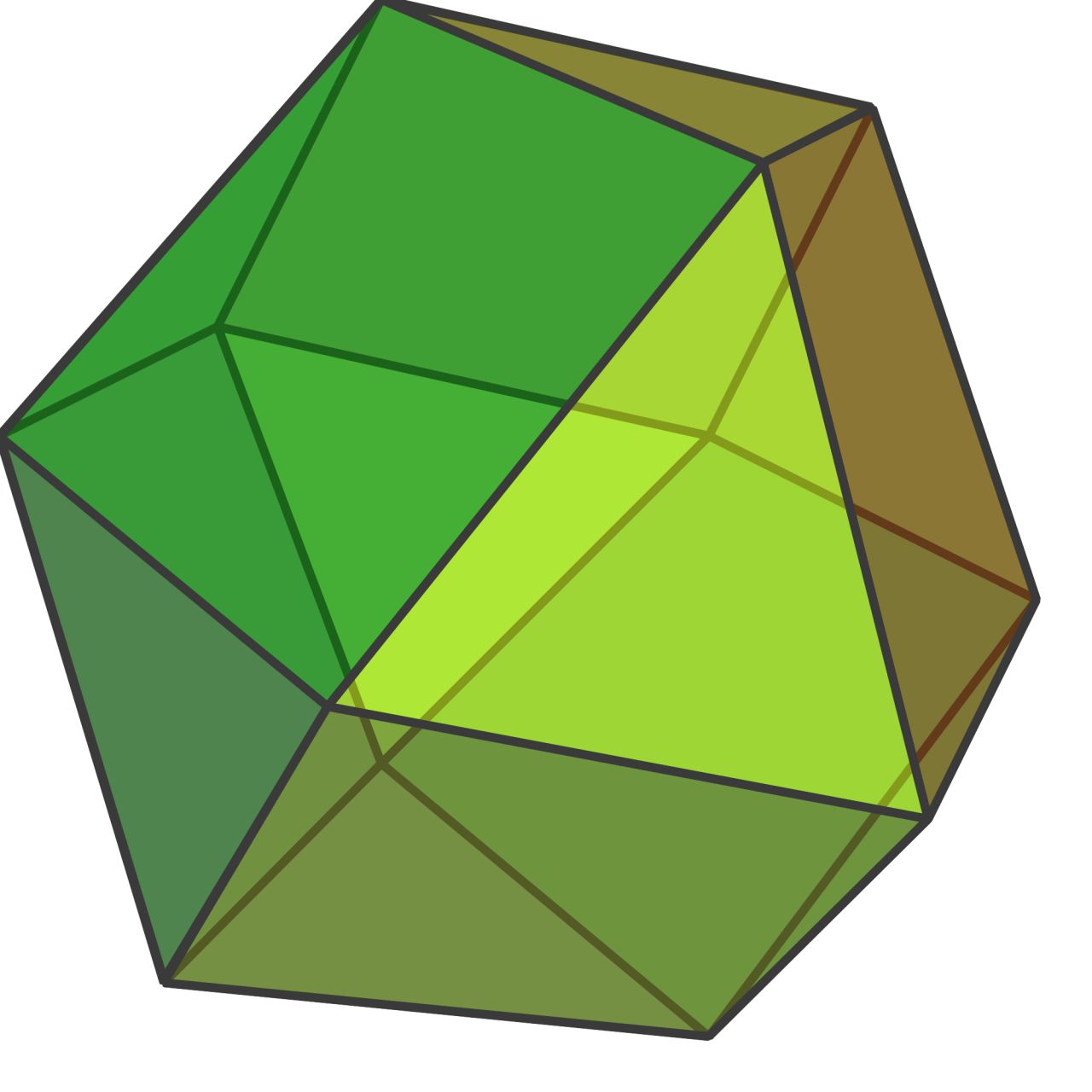 |