正多胞體定義：
它是一個四維空間上的多胞形(Polytope,點、線段、多邊形、多面體，以及更高維度的幾何物體的總稱)
多胞體表面(Facet)由有限個正多面體組成，每個頂點情況相同
專業點說，就是每一個頂點圖(Vertex figure)都是正多面體
簡單而言，就是正多胞體中每一條棱外一點旋轉一圈，都會穿過相等數目的面（或體）

一個關於正多面體二面角的列表：


考慮到正多胞體里正多面體必須是有限個的，因此一條棱上的幾個面的相鄰夾角總和（棱上所有多面體的二面角之和）必須小於360度
60°≤70.53°<72°，可知由正四面體組成的正多胞體有三個，分別是每條棱上有三個、四個和五個正四面體，分別對應施萊夫利符號{3,3,3}、{3,3,4}、{3,3,5}
90°≤90°<120°，可知由立方體組成的正多胞體有一個，它的每條棱上有三個立方體，對應施萊夫利符號{4,3,3}
90°≤109.47°<120°，可知由正八面體組成的正多胞體有一個，它的每條棱上有三個正八面體，對應施萊夫利符號{3,4,3}
90°≤116.57°<120°，可知由正十二面體組成的正多胞體有一個，它的每條棱上有三個正十二面體，對應施萊夫利符號{5,3,3}
120°≤138.19°，可知不存在由正十二面體組成的正多胞體

綜上可得正多胞體一共有6個：{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Pentachoron
正五胞體(5-cell)，又作正四面體錐(hyperpyramid)，4-單形（4-simplex）
其施萊夫利符號是{3,3,3}，頂點圖(Vertex figure)是正四面體，在正五胞體中每條棱上有三個正四面體
一般而言，它是正四面體的四維類比
下圖是它的施萊格爾（透視）三維投影圖，下同：

及球極投影圖，下同：



正多胞體里的多面體數（還有頂點數、棱數、面數）都是根據這兩個圖「數」出來的
正四面體胞：5，正三角形面：10，棱數：10，頂點數：5
平行投影圖（二次平行投影，由四維通過平行投影至三維，再由三維平行投影至二維）


所有正多胞體中最簡單的了，作一個正五邊形，讓五個點兩兩連線即可

一個正五胞體的正面圖：


一個正五胞體的旋轉圖：

補充：正五胞體帶投影面的球極投影：






Tesseract
把一個正方形向第三方向（向上）推移就得到一個立方體，同樣把一個立方體向第四方向推移，就會得到一個超立方體
超立方體，又作正八胞體(8-cell,Regular octachoron)，立方體柱(Cubic prism)，4-4邊形柱(4-4 duoprism)
另：「超立方體」的英文是Tesseract而不是Hypercube，Hypercube在wiki上是指N維立方體（一維的線段，二維的正方形，三維的立方體……）的總稱

Tesseract，立方體胞：8，正方形面：24，棱數：32，頂點數：16
它 的施萊夫利符號有幾個{4,3,3}(特指它是正多胞體Tesseract);{4,3}x{}（代指Cubic prism）;{4}x{4}(4-4 duoprism);{4}x{}x{}（代指Square prismatic prism）;{}x{}x{}x{}（代指Line segmentary prismatic prismatic prism，這個……）。頂點圖是正四面體，在超立方體中每條棱上有三個立方體
不用說，它就是立方體的四維類比






像立方體6個面展開一樣，超立方體的展開圖：


平行投影：


在平面上畫四根軸，其中相鄰軸的夾角為45度(每根軸的單位長度相等)，再在平面上標出超立方體的十六個頂點(±0.5,±0.5,±0.5,±0.5)，然後連線（表達很繁瑣，過程很簡單）
超立方體的旋轉圖wiki上有很多，個人覺得下面這個最好

我現在才發現當年寫這種東西的時候表達能力有多麼糟糕
不說了，照發
 
Hexadecachoron
將一個正方形不相鄰的兩點連線，得到一個正二邊形(Demisquare)；將一個立方體兩兩不相鄰的四個點沿各自的面連線(Demicube)，得到一個正四面體；同樣地，將一個超立方體兩兩不相鄰的八個點沿各自的面連線後，正好會得到它的對偶——正16胞體
它穿過我們空間的時候我們會看見一個又零開始勻速增大的正八面體，一段時間後又以相同的速度縮小，直到消失，這便得到一個正16胞體

正十六胞體(16-cell)，又作正四面體反稜柱(Tetrahedron antiprism)、
又作Tetracross（四維交叉多胞形(?)，日文「4-正軸體」，沒有中文翻譯）、
又作4-orthoplex（也沒有中文翻譯，一個N維的orthoplex和cross都指代同一個多胞體，但意義不同）、
又作Demitesseract（照樣沒有中文翻譯，指代第一段超立方體上連線得到的東東，暫時稱為半截超立方體）

16-cell，正四面體胞：16，正三角形面：32，棱數：24，頂點數：8（因為是超立方體的對偶，所以它的數據剛好是反過來的）
它的施萊夫利符號也有幾個，{3,3,4}（特指它是正多胞體16-cell）；（特指它是orthoplex，代指Demitesseract）；h{4,3,3}（alternated[*] tesseract）等等
其頂點圖是正八面體，正16胞體每條棱上有4個正四面體

16- cell可以通過兩種類比方法得到，一種是正八面體的四維類比（正八面體是立方體對偶，頂點為(±1,0,0) 的全排列；而16-cell是超立方體對偶，頂點為(±1,0,0,0) 的全排列），另一種是正四面體的四維類比（上面第一段，正四面體是半截立方體，這不是一個正多胞形的類比方法）

另外，由於正16胞體的二胞夾角為2arctan√3=120°=360°÷3，因此單用正16胞體可以組成一個四維堆砌（相當於二維的均勻鑲嵌tiling、三維的均勻堆砌honeycomb）施萊夫利符號{3,3,4,3}，每個二維的面上有3個正16胞體





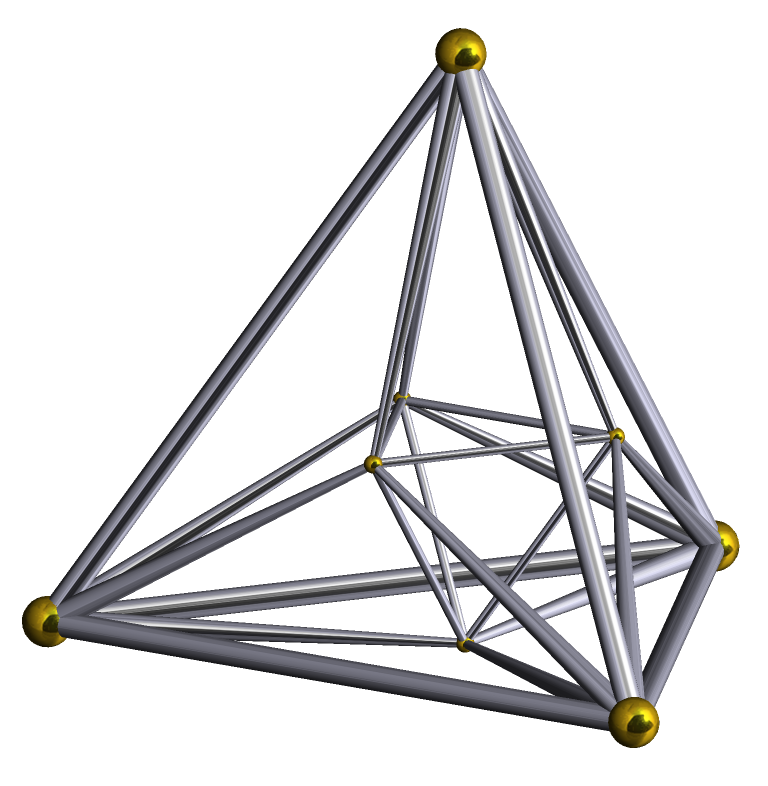
平行投影

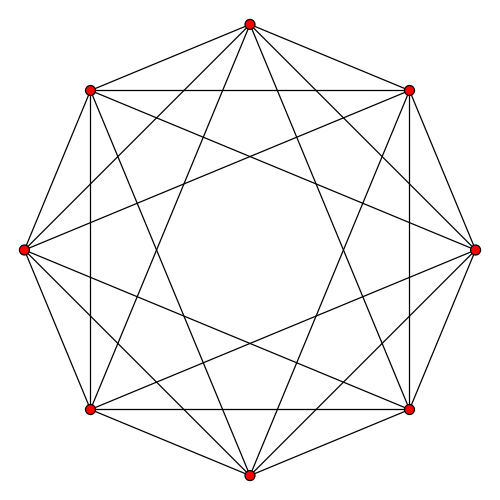
同超立方體一樣的方法，畫四條軸，標上 (±1,0,0,0)、(0,±1,0,0) 、(0,0,±1,0) 、(0,0,0,±1)八個頂點在連線（作法比超立方體簡單多了）

最後是旋轉圖

回復：5樓

那個沒顯示出來的小圖像是：

Icositetrachoron
正二十四胞體(24-cell)，有時又作復正八面體(octahedral complex)，是唯一一個沒有三位類比的正多胞體
24-cell，正八面體胞：24，正三角形面：96，棱數：96，頂點數：24（注意到胞數和頂點數，面數和棱數也相等——與正五胞體一樣，它也是自身對偶的）

它的施萊夫利符號也有幾個，{3,4,3}（特指它是正多胞體24-cell）；（特指它由16-cell截角得到，代指Rectified 16-cell）；（特指它由Demitesseract截角得到，代指Rectified demitesseract——這個東西要涉及Coxeter–Dynkin diagram的，看的懂的求陪同）
其頂點圖是立方體，正24胞體每條棱上有3個正八面體

一般而言正方形是24-cell的二維類比，根據它們的施萊夫利符號推算（略）知道，一定意義上它是截半立方體（半正多面體）或菱形十二面體（卡塔蘭立體，半正多面體的對偶）

另外，由於正24胞體的二胞夾角也是120°（推導過程不詳），因此單用正24胞體也可以組成一個四維堆砌，施萊夫利符號{3,4,3,3}，是{3,3,4,3}。每個二維的面上有3個正24胞體


（帶投影面）

平行投影（作法不詳）：

一種沒有線條重合的二維投影（非正多邊形外框）


旋轉圖：


一個24-cell穿過三維空間（太快了，我也沒看懂）


補充：分層結構
正如正二十面體一樣，表面越複雜的立體分層越明顯，以正二十面體的一個面（準確地說是把它的表面都膨脹成球後的一個面上）為極點，將緯度相同的幾個面記作同一層，那麼正二十面體可分作1-3-6-6-3-1六層（有興趣的筒子可以拿個正二十面體模型玩玩）。
 
同樣地，正二十四胞體也可以這樣分，共五層。不過緯度已經不再指一根線了，而是指四維球表面上的一個「緯面」了
1 cell   相當於北極點  
8 cells  約莫北緯面60°處  
6 cells  赤道面
8 cells  約莫南緯面60°處
1 cell   相當於南極點

Hecatonicosachoron
（最複雜，也是最解說不能的兩個來了）
正一百二十胞體(120-cell)，又作復正十二面體(Dodecaplex=Dodecahedral complex)，超正十二面體(Hyperdodecahedron)
120-cell，正十二面體胞：120，正五邊形面：720，棱數：1200，頂點數：600
其施萊夫利符號是{5,3,3}，頂點圖是正四面體，在正120胞體中每條棱上有三個正十二面體
一般而言，它是正十二面體的四維類比

另 外，由於正120胞體和正600胞體的二胞夾角太大（推導過程不詳，我只知道大於120°），因此它們是沒辦法向更高維度繼續類比的，正120胞體的五維 類比是一個坐落在四維的雙曲堆砌(Hyperbolic honeycomb in 4 dimension)，每個面上有三個正120胞體

再另外，根據120-cell的600個頂點重新連線「連面」可以得到十個星形正多胞體的其中一個（Great grand stellated 120-cell）



（帶投影面）


平面投影（作法：小的連中等數學都沒學完，你問我我問誰）（不過話說回來，這種圓盤結構倒挺美妙的）：


補充：
分層結構，這點在複雜120-cell和600-cell上體現的很明顯
這裡我照抄維基百科的，不改緯度數了，裡面的緯度數都是以北極為0度南極為180度的
1 cell     0°
12 cells   36°  
20 cells   60°  
12 cells   72°  
30 cells   90°
12 cells   108°
20 cells   120°  
12 cells   144°  
1 cell     180°
拿出其中幾個正十二面體表面來看的雙環


120-cell的二胞角是144°，求法http://tieba.baidu.com/f?kz=1046741707  
最後是旋轉圖，文件很大，要小心

竟然有內部結構的旋轉圖

Hexacosichoron
正六百胞體(600-cell)，又作復正四面體(Tetraplex=Tetrahedral complex)，超正二十面體(Hyper-icosahedron)
600-cell，正四面體胞：600，正三角形面：1200，棱數：720，頂點數：120
正600胞體與正120胞體互為對偶,其施萊夫利符號是{3,3,5}，頂點圖是正二十面體，在600-cell中每條棱上有五個正四面體
一般而言，它是正二十面體的四維類比

另外，正600胞體的五維類比也是四維的雙曲堆砌，施萊夫利符號是{3,3,3,5},與正120胞體的五維類比{5,3,3,3}對偶，它每個面上有五個正五胞體
再另外，根據600-cell的頂點重新連線「連面」可以得到十個星形正多胞體的另外九個（見下一樓）

這 是一個vertex-centered的施萊格爾投影，就是說這個傢伙看600-cell眼睛是正對著一個頂點，而不是向前幾幅圖那樣正對著一個多面體胞 的——其實這個vertex-centered投影如果放在球極投影上這個傢伙看著的頂點就該處於無限遠了，而在這裡這個頂點則很不厚道地放在三維投影的 中心


（帶投影面）


二維線架，做法同上一樓

補充
分層結構
600-cell的分層略顯犀利了，有31層！
依次是1-4-12-24-12-4-24-24-32-24-12-24-28-24-24-54-24-24-28-24-12-24-32-24-24-4-12-24-12-4-1
分層見http://davidf.faricy.net/polyhedra/Polytopes.html
最後是旋轉圖，也很大，小心！