不定積分是微分的逆運算，不是求導的逆運算，所以積分符號後面當然要跟上微分的運算結果（也就是微分式）。例如0，(4+x)dx，7dx等都是微分的運算結果，而8則是求導的運算結果，不是微分的運算結果，所以∫8是沒有意義的。注意4+dx不是微分運算的結果，因為沒有哪個函數隻進行微分運算後能得到4+dx，必須要先微分再進行一次加法運算才能得到。
設p = 4xdx，那麼d(2x²)=p，也就是說對2x²進行微分運算後，其運算結果是p。由於不定積分是微分的逆運算，那麼∫p肯定就等於2x²。
再看下面的例子：

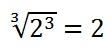
可以看出開方符號裡面也有乘方運算。若f(x)=x³，並規定符號√為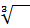（也就是∛），那麼上式就可以寫為√f2=2，也可以寫為√8f1=2，並且8f1=f2。這個就和∫d(sinx)=sinx，∫cosxdx= sinx，d(sinx)=cosxdx很相似。
若有方程8fx=f(7+3x)，那麼兩邊進行√運算：√8fx=√f(7+3x)，因為8fx=f(2x)（這個根據√的運算性質可以得到），所以可以得到：2x=7+3x，因此x=-7。這個非常類似於解微分方程。
那麼為什麼√8有意義，∫8就沒有意義了呢？這是因為8可以是乘方運算的結果，但卻不可能是微分運算的結果。

我覺得，課本上在講不定積分的時候壓根就不該提到求導。直接說，不定積分是微分的逆運算。因為d(2x³)=6x²dx，所以∫6x²dx = 2x³；因為d(3x²)=3d(x²)，所以∫3d(x²)=3x²；因為找不到一個函數使d(?)=6x，所以∫6x無意義。然後說∫6x²dx裡面的6x²dx叫做被積表達式，不說6x²叫被積函數。這樣的話肯定就沒人再問dx是什麼了。