綜述：經典力學又叫經典運動力學，是以牛頓定律為基礎來研究相對運動及運動改變的原因的物理學分支。
其他相關力學分支參見2樓連結。


基本概念：
【時間】
古典時間觀念：時間是用於描述 事件發生的先後順序 和 物質變化的連續性 的標度
我們通常所說的時間一詞指包括所有可能存在的時刻，是由所有可能存在的時刻組成的整體（數學上的一個集），這是時間這個詞的主義
此外，時間一詞通常可能還指代下述三個具體概念：


1----時刻（時序標）：
用於描述事件發生的先後順序，忽略連續性成分，在有必要考慮其連續性成分時，通常被視為」瞬間「，在將時間視為一維單向軸概念時，時刻被視為時間軸上的一點
時刻的相對性：
計時器何時開始計時，計時器的走率快慢都會影響測量者對時刻的計數（測量）
例如：每個人的手錶未必與國家標準計時鐘表完全一致，但我們說即使如此，每個人用自己的鐘錶測量時刻，並將其作為參考數據代入相關物理問題，都不會影響問題最終結果的正確性，具體原因參見與時刻的相關物理定律


2----時間差：
任意兩個時刻之間的差值，通常用時序上偏後的時刻減去時序上偏前的時刻得到這個概念，而不是反過來減
請注意，這個概念是個純數學概念，並不具有實際的物理意義，因為它並不限定兩個時刻必須是同一觀察者測量的，也不限定兩個時刻必須是在同一地點測量的，而當我們對運動力學稍有了解之後你會發現，這兩個具體要求其實非常重要，它們將導引出下面一個重要概念：


3----時段：
時段是一種時間差，但它不是任意的時間差，它有如下嚴格的要求：
同一位觀測者，在同一地點所測量得到的兩個時刻相減所得到的時間差（當然是按照時間差的定義，用時序上靠後的時刻減去時序上靠前的時刻得到的差值），叫做時段
時段用於描述被觀察者觀測的物質狀態變化過程的持續性，而不符合時段定義的那些任意的時間差都不能用於描述物質變化的連續性




上述三個概念為 時間 的歧義，加上時間的主義，時間一詞共計四個含義，在物理學書籍中通常都稱為時間，請注意根據語境自行區分

在中文物理書籍中，
時刻有時被稱作瞬時，這兩種叫法是同義的
時間差又是被叫做時長，這兩種叫法也是同義的
時段通常沒有另外的叫法，但很多時候會直接被稱為時間差或者時長，在不會對問題思考造成嚴重錯誤的條件下，我們默認這種稱呼是合適的，但從嚴格意義上來說這種叫法是錯的，尤其在相對論問題中


時間的測量定義（也叫物理定義）：
要定義時間的幾個概念，先要定義 鍾 的概念：
假定可以找到某種可以自發重複發生的物理變化過程，該種過程滿足條件：
1----每一次該種物理變化都能夠找到明確的變化起點事件和變化終點事件
2----同一次該種物理變化的變化起點事件和變化終點事件之間有持續性
3----每一次該種物理變化的變化起點與其前一次該種物理變化的變化終點間沒有持續性（或稱之為在時序上重合）
4----不同次的該種物理變化所對應的連續性都相同
5----該物理變化是不可逆的
則可以認為我們找到的這種能自發重複發生的物理變化具有」周期性「或」均勻性「
滿足這種要求的可自行重複發生的物理變化過程，即可被視為一個」鐘錶（簡稱鍾）「過程
下面我們定義時間的三個具體概念：

時刻：
鍾過程的每一次重複發生的起點事件就是上一次過程的結束事件，因此我們把每一次鍾過程的起點事件用實數來標定為一個時刻，並用實數的大小關係來表示各次鍾過程的起點之間的時序先後關係
通常我們認為時刻不具有持續性，因為它所對應的鐘過程的起點事件是被視為沒有持續性的，因此才可以在數學上對應於一個確定實數單值

時間差：
時序靠後的時刻值減去時序靠前的時刻值得到的數學差值
在很多情況下，所謂時序靠後指的是時刻對應的實數值較大，很多時候而並不是真的考慮具體時序關係，因為不同參照系的時刻之間不一定能很輕易確定時序先後，而同一觀察者在不同地點測量的兩個時刻之間未必描述同一個物理過程，但是物理學中仍然要求儘可能地在確定了時序先後順序之後才去做差

時段：
同一觀察者在同一地點測量的兩個時刻，按照時間差定義相減得到的數學差值

【空間】
古典釋義：容納物質存在的範圍稱為空間


這個古典釋義並不能夠在物理中準確應用，因為我們目前尚不清楚某些物質屬性確實是獨立的物質屬性，還是我們觀測<高維空間結構在我們三維空間中的投影>時獲得的觀測效應
直白一些來說，我們不知道是否真的存在更高維的空間結構，所以空間這個詞是否僅限於指代三維空間，還是一個有爭議的問題
但在現代理論物理學中，物理學家傾向於認為高維空間結構存在，而很多物理屬性實際上是我們觀測<高維空間結構在我們三維空間中的投影>時獲得的觀測效應，因此在諸如弦論之類的物理學專著中，空間一詞可以涵蓋超過三維空間的領域


儘管空間這個概念並不是一個準確的概念，但並不影響我們用測量手段給出與之相關的一系列物理概念的準確定義：


【尺】
在討論時間的時候，我們定義了時間測量工具」鍾「的概念，在這裡的」尺「顯然是空間測量工具的概念（之一）
首先，尺也具有確定方向性
在數學上，連續曲線（一維）通常指光滑連續的曲線，我們可以對曲線規定出它的自然坐標系：
即給曲線上每一點指定一個實數值，並要求所有點的實數標度（坐標）應該是按照實數大小順序遞增排列，形成曲線上的自然坐標系，並以此給出曲線的坐標遞增方向
尺上的方向概念類似曲線上方向的定義，尺也具有類似曲線的自然坐標系，所以尺上也有坐標


其次，尺也具有容納的屬性

容納屬性通常在理論意義上被稱之為」連續性對坐標變數可求導「。這個解釋起來稍微有點麻煩：
數學上的連續曲線，並不都指光滑連續曲線（一維），還有分形曲線（非一維曲線，例如某些看似噪波的具有無窮精細結構的曲線）的存在，分形曲線也屬於連續曲線
但是光滑連續曲線的連續性（這裡我們還沒有給出長度的概念，所以還得說連續性，其實這裡隱含了長度概念）在數學上是能夠對坐標求導數的（準確說是長度能對坐標求導）
而分形曲線則不一定都能滿足：其連續性（長度）能對任意一點坐標求導，甚至它們的長度定義也不那麼簡單
因此我們要求我們的尺必須是一維連續曲線型的，即」連續性對坐標變數可求導「的
其實當我們在後面介紹了長度定義之後，各位會更直觀地明白：
要求尺能夠滿足」連續性對坐標變數可求導「，其實就是為了能在尺上定義長度
當我們的尺滿足了」連續性對坐標變數可求導「這個要求，我們可以對尺取任意兩段，即找至少個4坐標點a,b,c,d（我們假定三點坐標遞增a<b<c<d），它們沿著尺的坐標增大方向可以形成兩個坐標差b-a和d-c（大值的坐標減去小值的坐標）
當我們把b-a平移到d-c的位置去，我們的尺應該滿足如下條件：
如果在數學上b-a=d-c
那麼我們在尺上所做的平移應該導致原來的a點移動到c點，即a和c重合；且同時有另一結果：
原來的b點移動到d點，即b和d重合
簡單來說就是數學上相等的差值對應尺上坐標之間的尺的部分的空間容積相等
我們要求對任意坐標a<b<c<d，在b-a=d-c時，我們的尺都一定滿足平移b-a到d-c之後，a和c重合，且b和d重合
這樣的一件一維測量工具，就叫 尺，它滿足」純量平移不變性（就是我們上面要求的平移後一維容積相等）「


最後要說的是，別忘了尺可能有形狀，我們也沒有定義一定必須是直尺（這個觀點在相對論這類非歐幾何時空理論中尤為重要），尺對應的曲線也可能會與自身相交（形成某種循環結構），原則上來說，上面對於尺的定義有一定通用性，當然在具體問題中可能還要有修正（我們在這裡就不涉及修正的問題了），但我們要清楚的是，上述定義暗含了一個條件：
尺可以在平移過程中改變形狀，以保證尺上的點與被測一維空間部分的端點重合
我們的尺能夠在任意變形的情況下依舊滿足」純量平移不變性「，這是尺的實質特徵


【長度】
長度一詞專指空間長度，而在時間概念中有時長的說法，長度是物理學上對於一維空間部分的容量的描述，而實際上它也暗含了空間連續性（這個是通過尺的數學可導性暗含的，我們不重複說了）
在我們上述定義的尺的概念之下，如果我們用平移這把尺，使被測量的一維空間部分的至少2個端點與尺上兩點分別重合（注意我們的尺可以任意變形來適應被測一維空間部分的形狀），那麼尺上這兩點的坐標（每點一個，共計兩個坐標）就可以按照其坐標值，大值坐標減去小值坐標得到一個數學差值，這個差值一定不是負數，它稱為長度


由於尺實際上是可以任意變形的，所以我們所說的長度當然包括直線和曲線長度

【角度】

通常我們這裡指的是二維空間的角度，但很多時候它也會被擴展到三維空間中去使用，比如數學中的空間曲線夾角或者曲面夾角（實質上都是二維空間的角度）
定義這個概念之前，我們有必要談一談二維空間（我們不涉及更高維數，而且我們要提醒大家的是，我們下面的討論最多能夠適用到三維空間，四維空間或更高維空間，已經不能憑直觀來想像）


一個二維空間，數學上的抽象定義是空間中每一個容量為0的結構（我們不直接說是點，因為可能導致其他問題，例如點的鄰域的連續性問題，我們不想討論那麼多太複雜的與本部分主題無關的東西），可以用兩個坐標來定位


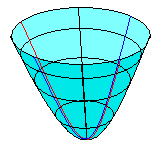
例如圖中曲面上任意一點可以用經向坐標（通過該點的拋物線上的自然坐標系中的坐標）和緯向坐標（通過該點的圓線上的自然坐標系中的坐標）這兩個坐標來定位

但是我們很容易想到一個問題，經緯向的自然坐標系都是一維坐標系，它們要組成一個二維坐標系，必然要有一套組成規則
如果你想到了這個問題，那麼就表明你觸及到我們問題的核心了：
一個二維結構絕不是一系列一維結構的隨意組合，二維結構之所以不再是一維結構，就是因為它上面存在了新的空間結構規則
所以我們討論二維空間中的位置關係的時候，不僅要討論長度（距離），通常還要討論角度，因為角度是用來描述一維空間結構如何組成二維空間結構的規則用到的概念


物理學中的二維角度定義，與幾何中二維角度定義一致，當兩條曲線相交時，我們取它們交點附近的兩條曲線的儘可能小部分（都要包括交點在內），將所取的兩部分（每條曲線取一部分）近似看作直線，這樣確定了一個非常微小的平面結構，在這個平面結構中去根據根據平直空間結構下定義的角度概念來定義兩條直線之間的夾角


所以最終我們還是要定義平直空間中的兩直線夾角


說到平直空間，很多人認為首先是一維平直空間的概念，即直線的概念，實際上我們並不能孤立定義一條直線，因為直這個概念本身由角度來定義，在我們沒有定義角度前，扯直線的概念就等於是循環定義（角度由直線定義，直線又由角度定義，實際上兩者都是架空的定義）
所以我們首先討論的是面結構（未必是平面，因為你還沒定義角度，平面的平也是靠角度定義的，但是曲面不需要依靠角度來定義，所以說曲面更具有一般性）
我們還要強調的是我們這裡談論的曲面都是光滑曲面，它不僅由光滑曲線構成，而且所有構成它的光滑曲線之間的組織方式也是光滑的（這不是數學語言，數學語言會涉及到各種可導性，還會考慮到那些分形曲線和分型面結構，那對我們來說太複雜，而且和本主題沒多大關係，所以我們用一種不太專業但比較直觀的說法來描述這個問題）
當我們隨意取曲面上任意小的一個部分，這個小曲面內肯定包含了兩條小的相交曲線，它們只有一個交點（如果不止一個，那說明我們取的小曲面還不夠微小，還要更小，直到只剩下一個交點）
在這種條件下，我們要求所取的」小曲面「滿足：
所有通過這兩條小曲線的那個交點的小曲線之間都不再有另外的交點
通過這個共同交點的所有小曲線形成一個曲線族，我們將它們稱為經向曲線族，我們可以將它們共同的交點定義為原點，其經向坐標為0，即所有小曲線上的一維自然坐標系都把這一點作為0坐標點重新規劃坐標系，而且我們知道原點把每一條經向曲線分為兩部分，一部分的坐標沿著曲線正向增大，一部分的坐標沿著曲線負向減小

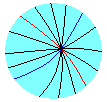
把一個我們選好的小曲面部分放大後的樣子，紅線和藍線為我們最先選取的那兩條線，黑線是和它們通過同一交點的曲線族（的幾個代表成員）



然後我們以那個交點為中心，畫一個任意的圈（形狀可以不規則，但仍然必須是光滑曲線，既然說它是圈，那就必須是條封閉曲線），並保證它絕對不通過那個交點：

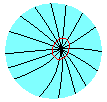
類似地我們還可以畫更多的圈，並且加一條要求：
所有的圈之間都沒有交點

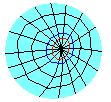
假定我們畫了無數個圈，它們可以稱之為同心圈族，也是一個曲線族，我們把它們稱為緯向曲線族，然後我們給出一個新規定來調整緯向曲線族：
同一條緯向曲線圈與所有經向曲線有且只有一個交點，這一系列交點與經向曲線族的原點（也就是緯向曲線族的共同的中心）之間的長度都相等（請注意這裡用到了前面說的曲線長度的概念）


這樣我們重新做一些規定：
1-----同一條緯向曲線圈上所有的點的緯向坐標（紅）都相等
2-----同一條經向曲線上所有的點的經向坐標（藍）都相等
最後就是這個樣子：

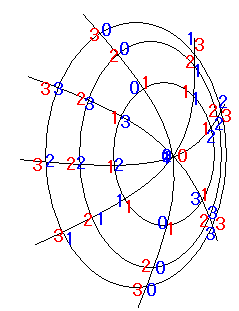
原點的經向坐標是任意的，但緯向坐標是0（確定的）
這個類似我們地球儀上的經緯網路，經緯網路就是用經緯兩個曲線族來規劃球面的二維坐標系，只不過坐標的數值設定和我們這裡不同


【注】別看我圖中畫的緯線圈全是橢圓，實際上可能是不規則的光滑封閉曲線形狀，別忘了我們是在曲面上說事，我們的曲面可能各種凹凸不平，我畫成橢圓只是為了畫著省事

另外，原則上來說，當我們選取的小曲面足夠小時，它已經近似為平面了，但是我們為了讓大家時刻記得我們是在曲面上說事，所以我畫的還是曲面（有些誇張）

現在我們要定義 類似平移 和 局域平面 的概念：
當我們在之前取的那個小曲面上建立了一個經緯坐標系之後，我們嘗試在這個小曲面上移動這個經緯坐標系，即保持它的面結構（我們之前總結的兩條規定）關係不變來移動整個經緯坐標系
移動後的小曲面上新舊坐標系位置我們用不同顏色標出（紅新藍舊）：

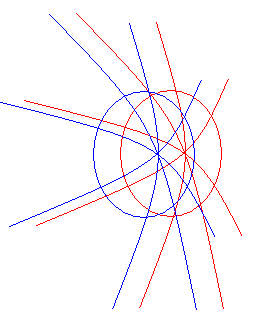如果我們所作的移動能夠保證任意同一條經向曲線（緯向曲線我們不在乎）在新舊坐標系位置上的兩個」分身「沒有任何交點（在我們的小區面區域內），我們稱這個移動叫 類似平移（物理中的平移都是類似平移，而不是數學中嚴格定義的平移）
如果我們把舊坐標系移動到小曲面內任意的位置時，都能找到至少一種 類似平移 的移動方式使新舊坐標系中同一經向曲線的兩個分身沒有任何交點（但不表示所有新坐標系中的同一條曲線的諸多分身之間沒有交點，因為有時候為了達到無交點的目的我們會對坐標系進行轉動，當然我們現在沒有定義角度，還不能用到轉動這個概念，但是你心裡可以大概有數，轉動的情況可能存在），我們稱這個小曲面是個局域平面


實際上在物理中，我們通常談到的平面，都是局域平面，我們不需要去研究數學中嚴格定義的真正的平面，局域平面對物理中的空間問題來說已經足夠用了


我們之所以要談經緯坐標系和類似平移、局域平面這些概念，是因為我們的主題」角度「需要這些概念來支撐，現在萬事俱備，我們進入正題：


假定現在有兩條相交曲線（注意不是我們前面說的微小曲線，是真正的大麴線）：

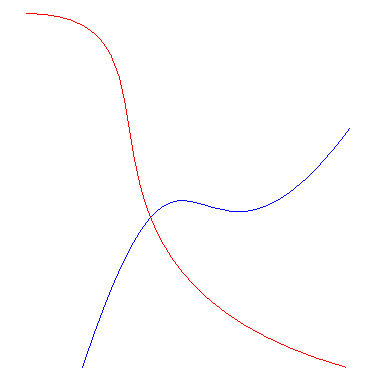它們有一個交點，我們想要知道交點附近的平面空間結構的情況，並以此來描述兩條曲線之間的位置關係（實際上是定義夾角）
那麼我們在交點處選擇一個儘可能小的小曲面，我們可以無限縮小選取範圍，使得選取的小曲面無限近似是一個局域平面（移動它內部一個任意的經緯坐標繫到它內部任意位置，新舊坐標系中同一條經線都沒有任何交點），並且我們以那個交點為原點建立一個經緯坐標系（要包括這兩條曲線在小區面內的部分也作為經線）

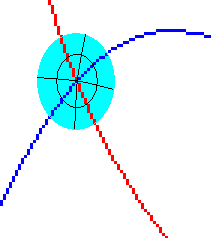我們定義：由原點某一側紅線為起始，其經向坐標為0，任找一條緯線圈，與該經線相交的點為起點（其經坐標當然是0），令緯線圈總長度為2π來標定緯線圈的一維緯向坐標系（經坐標系），按圖中方向（逆時針）令經坐標遞增

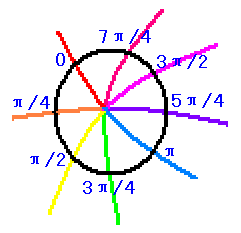過這條緯線圈上任意一點都一定有且只有一條經線，該經線的經坐標就是緯線圈的自然坐標系中該交點的坐標
實際上緯線上有無數點對應於0~2π之間的所有實數坐標，因此就可以有無數條經線分別於每一點處於緯線相交
則我們可以得出，按照逆時針方向來看，經線的經坐標在遞增，直到回到0經線為止（0經線即2π經線）


由此我們可以在經緯坐標系中找到最初藍線對應的經坐標9π/16：

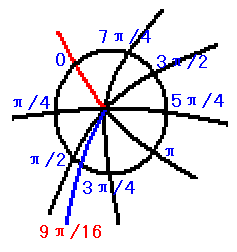實際上，由於藍線是曲線，而且當我們選取不同大小的緯線圈時，會與藍線有不同交點，按同樣規則來定義經緯坐標，小的緯線圈與藍線交點對應的經坐標可能與大的緯線圈不同

數學上通常規定：當選取的緯線圈越來越小不斷趨近於經緯坐標系原點時，按照上述方法給藍線找到的一個經坐標，在數學上會有一個極限值，這個極限值叫做」紅線到藍線的轉角「
它就是我們常說的兩條曲線之間的夾角的概念（與數學上用直線定義的夾角概念等價，但我們介紹的這種定義方法可以迴避掉直線、平面等概念，因為我們不想花篇幅定義這些無關的概念）
【注】經緯坐標系的定義過程其實類似於我們建立一個量角器你懂的

題外話：
我們為什麼要說類似平移，而不直接說平移，因為我們在曲面內移動坐標系，意味著坐標系不能跑到曲面以外的三維空間去，換而言之，被移動的坐標系是會自動變形適應曲面的，只是保持坐標系的那兩條規定不變，因此，這種移動可能不是真正的平移（保持坐標系各部分形狀不變）
而滿足局域平面要求的小曲面也未必就是真的平面，比如說我們可以把一張世界地圖上的南極部分繪製在一個平面上，也可以繪製在球面上，都不影響地圖的經緯坐標繫結構，而我們很清楚這個地圖顯然允許我們隨意移動經緯坐標系，保證經緯坐標系中同一條經線的新舊位置殘影之間」平行「，這個結論我們可以輕易從平面上繪製的南極地圖看出，它也同樣在球面南極地圖內成立
因此事實上我們單憑這種平移限定是無法絕對確定一張曲面是否是平面的


因此很多時候我們會懷疑，我們的三維世界是不是真正的平直三維空間，是否只是某種類似平直的三維空間，實際上只是更高維空間的一部分？
這個問題目前尚無答案，因為從整個宇宙的角度來看，我們周圍的空間就相當於一個局域的平直空間，它只能反映它附近的空間特性，而不能反映廣大空間的整體性質


所以我們說物理學中的平移都是指類似平移，而物理學中的平面都是指局域平面
類似地，直線也只是局域直線，三維立體也只是局域的平直立體空間


局域性是物理學中一個很深刻的主題，我們這裡只是稍帶提到它，說實話這只是冰山一角

待續

【物體長度】
提到物體的長度，我們回顧一下前述的空間長度（距離）的概念：
在空間長度（距離）概念中，我們定義的尺是會適應空間本身的彎曲形狀而變形的，例如一維尺可以在測量一維空間容量時，隨著一維空間（一維曲線）的形狀彎曲，因為尺就在這個空間內
但是當我們用尺去測量空間內的其他物體的時候，這就不是測量空間本身的容量了，尺是不會適應被測量物體的形狀而變形的，因為尺獨立於被測物體之外


例如我們測量一條曲線段的長度，我們定義這條曲線段的長度是當我們把它拉直之後，用直尺去測量它兩端坐標之間的坐標差得到的長度，尺不會改變自身去適應曲線段，而曲線段要做形變（哪怕只是理論上想像的形變，即用相關數學手段去獲取它被拉直的效果，參見微積分學中的曲線長公式）


我們這裡不會給出曲線長公式，我們只說說為什麼一個彎曲的曲線比直線要長，順便說說這個定理為什麼並不絕對成立


我們還是要具體說物體長度的測量，即我們是怎樣把一個彎曲物體拉直的
當我們默認測量者所在的空間為平直空間時，我們可以用勾股定理來很方便地說明曲線為何比直線長：

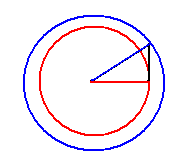圖中的紅橫線對應紅圓的半徑，藍斜線對應藍圓的半徑，我們知道圓越大對應它的半徑越長，所以藍線必然比紅線長
而之所以如此，是因為根據藍線長度公式：
藍線長度=√（紅線長²+黑線長²）
雖然黑線並不在藍線方向上，但黑色豎線對藍線長度有正值貢獻


而我們隨便看一條曲線，它可以近似為折線：

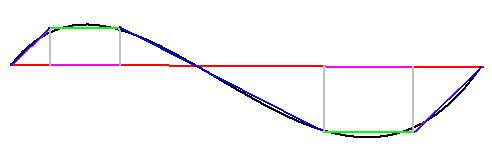綠線和粉線的長度都是一樣的，但藍線都比對應的紅線多了灰線的貢獻（類似前面勾股定理的例子），所以藍線都比紅線長，因此折線總長比橫直線要長，我們看到曲線的長度和折線很接近，因此可以很容易看出曲線要比橫直線長


在數學分支---解析幾何中，只要將曲線分割成做夠多的足夠小的部分，就可以把這些小部分近似成小折線（或者說是曲線各點處的一個微小的切線段），用曲線函數分別計算它們的斜率（即小折線位置處曲線函數對橫坐標的導數，對應於小斜線橫縱長度分量之間的比值），就能用勾股定理計算每一小段的長度，然後把所有微小的斜線長度相加得到整條曲線的長度，這是一個積分（積分就是對無數個微小單元的值求和，它相當於一個求和運算，只不過它的加數是無窮多個，所以它是個數學極限）


我們上面一段話其實已經給出了曲線長公式的推導思路，不過我們不想就這個話題說更多，有興趣的朋友可以自己去查資料






當一個物理問題擺在我們面前時，我們如何去判斷它要研究的是空間長度（距離）還是物體長度呢？
正如我們前面說的，當測量者本身處於被測物限定之下，例如我們被空間所容納，我們的尺也被空間所限制，這時我們的尺如果以空間本身的兩點間部分作為測量對象，那就是測量距離，尺要隨著空間本身的彎曲形態變形
如果被測物體並不能影響觀察者和他所用的尺，那麼這時測量的就是物體的長度，尺還是隨著空間本身的彎曲形態變形，而並不隨著被測物體的彎曲形狀變形
在經典力學中，這個區分並不重要，因為經典力學認定空間是平直的
在相對論中則認為空間會發生彎曲（有時間分量上的貢獻），因此做上述概念區分尤其顯得重要

【位矢（位置矢量）】
物理學中研究時間時通常忽略時間的方向，把時間視為一個純量（只有大小），因為我們默認時間的方向是單一不可逆的（這個目前為止還沒有發現反例）
物理學中的 位置 這一概念，則通常是個矢量（有大小又有方向的量），因為物理問題中空間方向至少為兩個（一維情況下），方向這個因素不能省略
舉一個最直觀的例子：
已知有一條走廊，維德的房門在走廊正中間，維德現在站在走廊中，他的位置就可以用一個矢量表示，即從維德的房門指向維德的一個矢量（方向），大小是房門到維德的長度（距離）
如果我們考慮更複雜的情況，例如地球上的一個衛星監測站正在監控繞地軸飛行的某一處於赤道平面上的衛星，那麼衛星的位置就是：

從監測站指向衛星的一個矢量，大小是此時監測站到衛星的距離，很方便吧


位矢的概念的最大優點並不只是用起來方便
我們看下圖：對於相同的一個位矢來說，無論我們以它的起點為原點規定何種坐標系統，這個位矢本身永遠是不變的，因此在物理中只要用位矢來確定位置，就可以在研究問題時完全不考慮坐標系環境，這會大大簡化問題的處理

因此，在物理學（尤其是理論物理）中，只要談到 位置 這個概念，通常說的就是位矢（位置矢量）
另外，矢量具有一個特點，它滿足平移不變性，即對這個矢量進行任意平移操作，矢量的大小和方向都不變（也就是矢量不變）
因此在研究物理問題時，可以通過平移矢量很方便地比較兩個矢量之間的大小關係和方向關係，位矢同樣可以用這種手段進行比較

【軌跡方程（軌道方程）】
試想把一個運動物體在每一時刻的位置點都畫在同一張圖中，一定可以形成一條運動曲線，物理學上把這條曲線叫做運動物體的軌跡
當我們以觀察者為中心建立了一個坐標系，那麼運動物體的這條「軌跡」中的每一點都可以在這個坐標系內定位（用位矢 或者 用坐標）
如果我們把軌跡中的每一點P的位置r與它對應的時刻t（請注意，物理書中有時會寫作「時間」，但你應該清楚「時間」在這裡專指時刻，而非其他時間概念）相對應，形成一個函數：
r(t)
這個函數叫做位置函數，表示點P的位置r隨著時刻t的變化而變化
當這個函數滿足某種數學條件P時，可以寫成方程形式：
r(t)=P
這裡條件P可以是常數或者函數（請注意：r(t)=P形式通常叫做 解形式，不是所有軌跡方程都一定要寫成解形式，相反地，絕大多數條件下軌跡方程都寫成非顯式形式，即其中根本不含有位置r這個變數，而是含有諸如坐標x,y,z等變數的形式）
那麼這個方程r(t)=P叫做物體的軌跡方程（軌道方程）


當我們用位置矢量r↑表示位置r時，該方程就變成r↑(t)=P，稱為位矢軌跡方程
當我們用坐標(x,y,z)等（還可以有其他類型坐標系下的坐標，例如球坐標或者柱坐標）表示位置r時，該方程就變成r(x,y,z)=P


例如一個勻速圓周運動的具體例子：

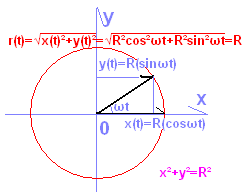紅色為軌跡方程（滿足條件是位置矢量的大小恆等於圓周半徑R），它是解形式的軌跡方程


藍色為軌跡方程的參數方程形式，即分別表示出了直角坐標系下橫縱坐標的方程並聯立成方程組，時間t為參數
粉色為消掉參數以後的軌跡方程
藍色和粉色這兩種非顯式（不明顯含有位置r）的形式才是最常見的軌跡方程形式