|
实际上都是空心的。 只是我们眼睛有问题 |
|
|
各位大大，需要两个四维公式
[圖片]
1.四维的点(x,y,z,w)在显示器上显示的方程(x,y) 2.四维的点(x1,y1,z1,w1)围绕另一个点(x0,y0,z0,w0)的旋转方程 
phevos1 7-19 183.213.56.*
(點擊/回復: 864/2) |
|
|
所以无论怎样放大一个圆，也找不到真正“平”的一个地方 所以无论怎样放大一个球，也无法真正找到一个完全平的地方
巨大八爪鱼 7-19 183.213.56.*
(點擊/回復: 759/3) |
|
 |
|
|
【图片】超正方体在三维超平面上的四视图
[圖片]
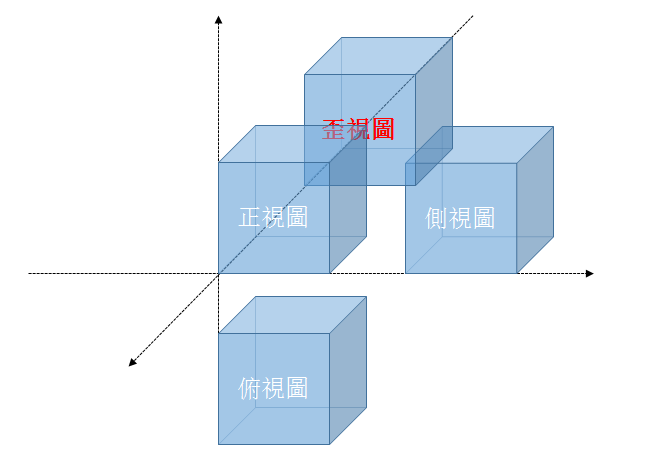
巨大八爪鱼 4-5 ----
(點擊/回復: 948/1) |
|
|
四维生物稍微移动一下其中一张正方体纸片，在我们世界中的三维人类就能看到两个正方体互相重叠了在一起了。 四维生物再稍微移动一下，两个正方体纸片又分开了。 |
|
|
图解超球北半球的三维投影
[圖片]
 |
|
|
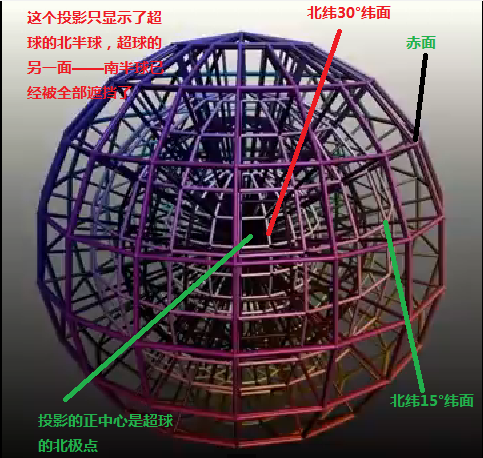为了让人们不去研究纯四维空间 |
|
|
前阵子读完了加来道雄（Michio Kaku）的《超越时空》（Hyperspace），对于高维空间、量子理论和超弦理论以及平行宇宙等有了粗浅的认识。在这里就很简单地介绍一下高维空间：...  |
|
|
这个纪录片对维度有比较基本的介绍和科普
Trisolaris 2-20 175.4.100.*
(點擊/回復: 804/3) |
|
|
我应该连四维爱好者都算不上，偶然间搜索到了四维的一些相关页面。 刚才刚睡醒的时候，突然想到，我们在二维的白纸上可以画出三维正方体在纸上的投影，被挡住的地方用虚线连接。那四维物体在三维空间上的...
112.227.230.* 12-30 巨大八爪鱼
(點擊/回復: 615/1) |
|
|
如果说三维空间加上时间是四维空间，那么问题来了，二维空间加时间是几维空间？一维空间+时间那？
101.231.198.* 12-19 114.46.48.*
(點擊/回復: 876/3) |
|
|
三维空间里平放的圆柱在2维桌面上 滚动方向是唯一的:垂直于它的旋转轴(或者高) ;四维空间中圆柱柱平放在3维桌面上，滚动方向也是唯一的:垂直于它的旋转平面(或者是两条高所决定的平面) ;而球柱平放在... |
|
|
这个图因为我没有专业工具所以没法画，但大体形状是：三维带经纬网的球体的正视图绕地轴旋转所形成的图形 |
|
|
其中正侧俯视图就是三维球体的三视图绕地轴旋转一周所形成的图形，一模一样。下面我们主要讨论超球的歪视图。（今晚暂时不发了） |
|
| 本吧共有主題數196個，帖子數830篇，四維愛好者數7位。 | |
|
內容轉換： |
|
