| 點擊/回復 | 標題 | 最後回復 | 發表時間/侃吧 |
| 250/0 |
多胞体各种维度的面的名称及简称
维度 全称 简称 0 零维面 点 1 一维面 线或棱 2 二维面 面... |
4-22 | 4-22 |
| 235/0 |
我认为影片中第三集的魔术黑板其实是三维平面普通黑板
也就是四维空间中的普通黑板，其表面是三维，所以能画三维图形 |
4-22 | 4-22 |
| 1600/13 |
【问答】“关于我们所在宇宙的几何结构的初步讨论”问答区
[问答区] 有看不懂的或有疑问的，可以到这里来问 |
9-29 121.225.146.* |
4-22 |
| 462/5 |
系统多面体：透视模型 这个不是已经上传了么
rt |
4-22 | 4-22 |
| 398/4 |
有没有三维星形多面体的图片和动画？
我要类比学习四维星形多胞体 |
4-22 | 4-22 |
| 378/1 |
通过五维单形的球极投影，可以数出有6个顶点
 |
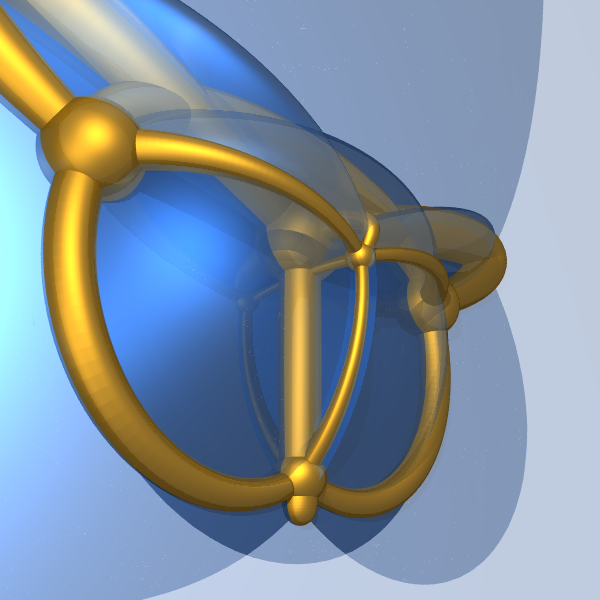4-22 | 4-21 |
| 370/1 | 【flash】1-4维的正方体 | 4-21 | 4-21 |
| 363/1 |
各种正多胞体的三维类比
5-cell：四面体 8-cell：正方体 16-cell：八面体 24-cell：无 120-cell：十二面体 600-cell：二十面体... |
4-22 | 4-21 |
| 1302/6 |
【动画】在四维空间旋转三维轮胎
 |
8-29 | 4-21 |
| 366/5 |
关于三维球面的横截面
二维的圆，可以由无数个从短到长，再到短的直线拼成 三维的球，可以有从小到大，再到小的二维圆拼成 那么，四维的球就是从小到大，再到小的三维球体拼成了 |
4-22 | 4-21 |
| 507/1 |
这个图不会就是四维轮胎吧？
 |
4-22 | 4-21 |
| 394/1 |
一道四维单形的证明题
任意五胞体EABCD自五个顶点分别引出四条直线（每个顶点不同颜色）使得自这一顶点引出的四条直线所组成的五胞体的各侧四面体所成二胞角分别为以
这一点为顶点对应的原五胞体EABCD各侧四面体所成二胞角的3...  |
4-22 | 4-20 |
| 629/6 |
【文章】关于拼四维球体
在二维空间中，我们给蜥蜴几个三维球体的横截面——即各种大小不同的圆，让蜥蜴在二维空间去拼三维球体，结果二维空间的蜥蜴根本拼不出来，他只是把各个圆摆在了一起，没有拼成真正的球体。 我们也一样，... |
4-22 | 4-20 |
| 319/2 |
三维超球面上是经面，纬面，而不是“线”
rt |
4-22 | 4-20 |
| 670/7 |
【图片】在三维空间中画正五胞体
先看看在二维的纸上画三维的正四面体。先画四个点，然后每个点两两相连，共画六条棱。 画出来后发现有两条棱相交了，但实际上根本没有相交。并且，后面的那条横着的棱被两个面挡住了，所以画...  |
4-29 | 4-19 |
| 438/9 |
我发现平行投影严重破坏了120胞体的形态，但球极投影就不一样了
平行投影严重破坏了120胞体的形态，导致各个正12面体互相相交，分不清谁是谁。 但球极投影后，各个12面体就挨个挨个的摆在一起，没有重合，很容易分辨。 当然超正方体也是一样的，直接... |
4-22 | 4-19 |
| 351/2 |
我认为在三维空间中任意选取五个点并两两相连画正五胞体更好些
就好比四维生物在三维平面上画正五胞体 |
4-22 | 4-19 |
| 339/1 |
貌似施莱格尔投影和球极投影都不是物体的原型
用手电筒照一个四维物体叫什么投影？ |
4-18 219.137.36.* |
4-18 |
| 295/0 |
【图片】正多胞体的三维展开图
http://zh.arslanbar.net/pictures.php?b=%E5%9B%9B%E7%BB%B4%E5%87%A0%E4%BD%95%E5%AD%A6&label=album... |
4-17 | 4-17 |
| 392/1 |
阿根廷大部分位于南温带
rt |
8-20 | 4-17 |
| 344/0 |
ubuntu11.04也没几天就发布了
rt |
4-17 | 4-17 |
| 397/1 |
话说我认为多维图形的二维线架图很像分形的说
并且维数越高分形图形越精细 |
4-17 | 4-17 |
| 525/2 |
【个人认为】4D文字和超正方体的推倒差不多
就是把3D文字复制一份，然后连接各个顶点 |
4-22 | 4-17 |
| 411/1 |
【问题】五维单形大概有多少个四维单形？
rt |
4-17 | 4-17 |
| 686/4 |
四次根号-1又是多少呢
rt |
7-10 183.213.56.* |
4-17 |
| 277/0 |
其实各种多胞体表面都是三维
不仅仅是超球 |
4-17 | 4-17 |
| 333/3 |
在百度搜索php，php官方网站www.php.net不知滚到哪一页去了。 而在谷歌就大不一样，把w
在百度搜索php，php官方网站www.php.net不知滚到哪一页去了。 而在谷歌就大不一样，把www.php.net排在了第一（mysql、apache均如此） |
8-19 | 4-17 |
| 459/3 |
这些是不是多胞体的展开图
24cell：  |
4-17 | 4-16 |
| 471/3 |
各种三维正多面体的球极投影都是jenn里面的
rt |
4-17 | 4-16 |
| 354/1 |
三维空间很容易想像
但三维平面就很难想像了，因为涉及到四维空间 |
4-16 | 4-16 |
等級：初級魔法師 五級
經驗：823點 金幣：155枚 性別：男 血型： 註冊時間：2011-3-18 23:49 最後訪問時間：2011-6-5 08:42 最後發帖時間：2011-5-18 13:45 個人簡介： |
帖子 |