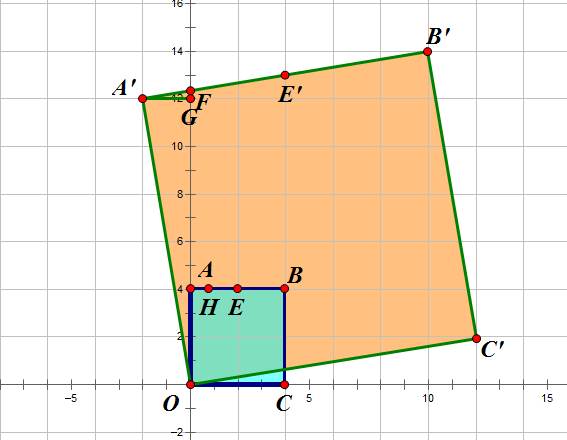如图，已知四边形ABCO和四边形A’B’C’O都是正方形，且B的坐标为(4,4)，AB=4，C’的坐标为(12,2)，求：
(1)     A’和B’的坐标；
(2)     若E’是A’B’的中点，求E’的坐标；
(3)     若A’B’交y轴于F，求△A’FD的面积；
(4)     若H是AB上一点，且A’F:A’B’=AH:AB，求H的坐标。

解：(1) C=B-ABi=(4,4)-(0,4)=4
k=C’÷C=(12,2)÷4=(3,0.5)
B’=Bk=(4,4)×(3,0.5)=(12-2,12+2)=(10,14)
A=B-AB=(4,4)-4=(0,4)
A’=Ak=(0,4)(3,0.5)=(0-2,12+1)=(-2,12)

(2) 作AB的中点E，AE=AB÷2=4÷2=2
∵A=(0,4)，∴E=A+AE=(0,4)+2=(2,4)
E’=Ek=(2,4)×(3,0.5)=(2×3-4×0.5,4×3+2×0.5)=(6-2,12+1)=(4,13)
 
(3)设A’B’的解析式为y=kx+b
则b-2k=12，10k+b=14
解得k=1/6  b=37/3
∴y=(x+74)/6
当x=0时
y=74/6=37/3
∴DF=37/3
作A’G⊥FD于G，则AG=2
∴S△A’FD=37/3*2/2=37/3
 
(4)           F=(0,37/3)
H=F/k=(0,37/3)÷(3,0.5)=(0+37/6,37-0)÷(9+0.25)
=(37/6,37)÷(37/4)
=[(37/6)×(4/37),37×(4/37)]
=(2/3,4)

话说这道题貌似连勾股定理都不能解。只能用复数解。

补充一下，点D就是点O

打错了

补充一道题：
(5)若正方形A'B'C'O的对角线交于点P'，求P'的坐标

回复：6楼

参考答案：

作正方形ABCO的对角线P,那么P的坐标为(2,2)，

则P'=(2,2)(3,0.5)=(6-1,6+1)=(5,7)