| |
點擊 |
回復 |
標題 |
作者 |
最後回復 |
| |
318 |
0 |
吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁p... |
4Der |
4-23 4Der |
| |
334 |
0 |
|
4Der |
4-23 4Der |
| |
325 |
0 |
复制本帖地址
回复数:70
点击数:102
本吧热门帖子
侃吧... |
4Der |
4-23 4Der |
| |
277 |
0 |
rt |
4Der |
4-23 4Der |
| |
324 |
0 |
0大事件jf0ujsadj0jf0osdj |
魔法绿骑士 |
4-23 魔法绿骑士 |
| |
317 |
0 |
|
4Der |
4-23 4Der |
| |
563 |
2 |
-i-1=(-1,-1)
设根号(-1,-1)=(x,y)
则
x²-y²=-1
2xy=-1 |
4Der |
4-23 yaoliding |
| |
572 |
9 |
上次说到维度时,有人提到了如何理解四维空间的问题。这是一个非常有趣的话题,可是我一直没有用心写一下。前段时间网上出了一部片子叫做Dimensions: a walk through mathemati... |
4Der |
4-23 118.117.5.* |
| |
699 |
0 |
http://zh.wikipedia.org/w/index.php?title=%E8%8D%AF%E5%AE%B6%E9%91%AB&variant=zh-cn |
Revive_ctg |
4-23 Revive_ctg |
| |
626 |
0 |
亲爱的用户:欢迎来到药家鑫吧,阿斯兰侃吧欢迎您的到来~
请先阅读我们的社区准则:http://documents.arslanbar.net/eula/zh/
以及版权声明:htt... |
侃吧管理员 |
4-23 侃吧管理员 |
| |
600 |
5 |
线:2×(12+4+6×4)+(8+1+6)=95
和影片不符啊,我少算了哪条线? |
4Der |
4-22 yaoliding |
| |
490 |
0 |
rt |
4Der |
4-22 4Der |
| |
503 |
4 |
若把四维球体球极投影到三维空间,就会占满整个三维空间(。。。)! |
4Der |
4-22 4Der |
| |
648 |
5 |
rt |
4Der |
4-22 yaoliding |
| |
406 |
0 |
维度 全称 简称
0 零维面 点
1 一维面 线或棱
2 二维面 面
3... |
4Der |
4-22 4Der |
| |
384 |
0 |
也就是四维空间中的普通黑板,其表面是三维,所以能画三维图形 |
4Der |
4-22 4Der |
| |
577 |
4 |
我要类比学习四维星形多胞体 |
4Der |
4-22 yaoliding |
| |
612 |
9 |
平行投影严重破坏了120胞体的形态,导致各个正12面体互相相交,分不清谁是谁。
但球极投影后,各个12面体就挨个挨个的摆在一起,没有重合,很容易分辨。
当然超正方体也是一样的,直接看平行投... |
4Der |
4-22 yaoliding |
| |
634 |
2 |
一个贴的内容太简单了,我觉得不如集中到一个贴里有想说的话的时候留个言
我希望这吧可以像四维空间吧那么多一点人去讨论一下 |
yaoliding |
4-22 yaoliding |
| |
826 |
6 |
在二维空间中,我们给蜥蜴几个三维球体的横截面——即各种大小不同的圆,让蜥蜴在二维空间去拼三维球体,结果二维空间的蜥蜴根本拼不出来,他只是把各个圆摆在了一起,没有拼成真正的球体。
我们也一样,给我... |
4Der |
4-22 yaoliding |
| |
516 |
2 |
就好比四维生物在三维平面上画正五胞体 |
4Der |
4-22 yaoliding |
| |
558 |
2 |
rt |
4Der |
4-22 yaoliding |
| |
570 |
1 |
任意五胞体EABCD自五个顶点分别引出四条直线(每个顶点不同颜色)使得自这一顶点引出的四条直线所组成的五胞体的各侧四面体所成二胞角分别为以
这一点为顶点对应的原五胞体EABCD各侧四面体所成二胞角的3...  |
4Der |
4-22 yaoliding |
| |
677 |
1 |
|
4Der |
4-22 yaoliding |
| |
755 |
2 |
正多胞体定义:
它是一个四维空间上的多胞形(Polytope,点、线段、多边形、多面体,以及更高维度的几何物体的总称)
多胞体表面(Facet)由有限个正多面体组成,每个顶点情况相... |
695223183 |
4-22 yaoliding |
| |
554 |
1 |
|
4Der |
4-22 yaoliding |
| |
703 |
2 |
就是把3D文字复制一份,然后连接各个顶点 |
4Der |
4-22 yaoliding |
| |
856 |
4 |
|
4Der |
4-22 yaoliding |
| |
535 |
5 |
二维的圆,可以由无数个从短到长,再到短的直线拼成
三维的球,可以有从小到大,再到小的二维圆拼成
那么,四维的球就是从小到大,再到小的三维球体拼成了 |
4Der |
4-22 yaoliding |
| |
551 |
1 |
5-cell:四面体
8-cell:正方体
16-cell:八面体
24-cell:无
120-cell:十二面体
600-cell:二十面体 |
4Der |
4-22 yaoliding |
| |
575 |
1 |
|
4Der |
4-21 4Der |
| |
229 |
1 |
|
64.34.204.* |
4-21 64.34.204.* |
| |
695 |
5 |
V4=a^4 |
218.88.141.* |
4-19 4Der |
| |
526 |
1 |
用手电筒照一个四维物体叫什么投影? |
4Der |
4-18 219.137.36.* |
| |
696 |
3 |
24cell:  |
4Der |
4-17 yaoliding |
| |
615 |
1 |
并且维数越高分形图形越精细 |
4Der |
4-17 yaoliding |
| |
642 |
1 |
rt |
4Der |
4-17 yaoliding |
| |
479 |
0 |
http://zh.arslanbar.net/pictures.php?b=%E5%9B%9B%E7%BB%B4%E5%87%A0%E4%BD%95%E5%AD%A6&label=album... |
4Der |
4-17 4Der |
| |
552 |
0 |
rt |
4Der |
4-17 4Der |
| |
747 |
4 |
我写的 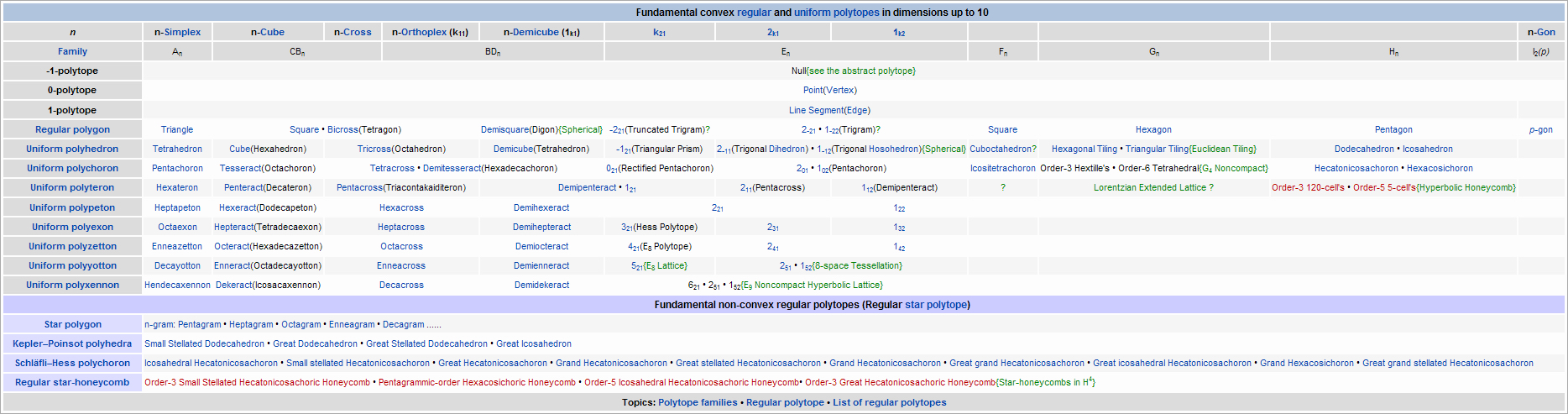 |
yaoliding |
4-17 4Der |
| |
701 |
3 |
rt |
4Der |
4-17 yaoliding |
| |
1172 |
7 |
今日:20帖 | 昨日:171帖
主题数:4877个 | 帖子数:12173篇
精品数:21... |
啊啊是谁都对 |
4-17 啊啊是谁都对 |
| |
479 |
0 |
不仅仅是超球 |
4Der |
4-17 4Der |
| |
652 |
1 |
http://www.tianya.cn/publicforum/content/develop/1/402518.shtml |
Revive_ctg |
4-17 Revive_ctg |
| |
316 |
0 |
亲爱的用户:欢迎来到百度吧,阿斯兰侃吧欢迎您的到来~
请先阅读我们的社区准则:http://documents.arslanbar.net/eula/zh/
以及版权声明:http... |
侃吧管理员 |
4-17 侃吧管理员 |
| |
644 |
5 |
http://zh.arslanbar.net/post.php?i=12737
你看,某人灌了那么多,都没被封过
但如果是百度那就不一样了,灌到200多层就会删帖+系统自动永久封禁... |
4Der |
4-16 yaoliding |
| |
767 |
16 |
http://zh.wikipedia.org/wiki/%E9%98%BF%E6%A0%B9%E5%BB%B7 |
Revive_ctg |
4-16 Revive_ctg |
| |
544 |
0 |
亲爱的用户:欢迎来到白鸽岛吧,阿斯兰侃吧欢迎您的到来~
请先阅读我们的社区准则:http://documents.arslanbar.net/eula/zh/
以及版权声明:htt... |
侃吧管理员 |
4-16 侃吧管理员 |
| |
562 |
1 |
但三维平面就很难想像了,因为涉及到四维空间 |
4Der |
4-16 yaoliding |
| |
609 |
1 |
= = |
114.224.159.* |
4-16 114.224.159.* |
|