综述：经典力学又叫经典运动力学，是以牛顿定律为基础来研究相对运动及运动改变的原因的物理学分支。
其他相关力学分支参见2楼链接。


基本概念：
【时间】
古典时间观念：时间是用于描述 事件发生的先后顺序 和 物质变化的连续性 的标度
我们通常所说的时间一词指包括所有可能存在的时刻，是由所有可能存在的时刻组成的整体（数学上的一个集），这是时间这个词的主义
此外，时间一词通常可能还指代下述三个具体概念：


1----时刻（时序标）：
用于描述事件发生的先后顺序，忽略连续性成分，在有必要考虑其连续性成分时，通常被视为”瞬间“，在将时间视为一维单向轴概念时，时刻被视为时间轴上的一点
时刻的相对性：
计时器何时开始计时，计时器的走率快慢都会影响测量者对时刻的计数（测量）
例如：每个人的手表未必与国家标准计时钟表完全一致，但我们说即使如此，每个人用自己的钟表测量时刻，并将其作为参考数据代入相关物理问题，都不会影响问题最终结果的正确性，具体原因参见与时刻的相关物理定律


2----时间差：
任意两个时刻之间的差值，通常用时序上偏后的时刻减去时序上偏前的时刻得到这个概念，而不是反过来减
请注意，这个概念是个纯数学概念，并不具有实际的物理意义，因为它并不限定两个时刻必须是同一观察者测量的，也不限定两个时刻必须是在同一地点测量的，而当我们对运动力学稍有了解之后你会发现，这两个具体要求其实非常重要，它们将导引出下面一个重要概念：


3----时段：
时段是一种时间差，但它不是任意的时间差，它有如下严格的要求：
同一位观测者，在同一地点所测量得到的两个时刻相减所得到的时间差（当然是按照时间差的定义，用时序上靠后的时刻减去时序上靠前的时刻得到的差值），叫做时段
时段用于描述被观察者观测的物质状态变化过程的持续性，而不符合时段定义的那些任意的时间差都不能用于描述物质变化的连续性




上述三个概念为 时间 的歧义，加上时间的主义，时间一词共计四个含义，在物理学书籍中通常都称为时间，请注意根据语境自行区分

在中文物理书籍中，
时刻有时被称作瞬时，这两种叫法是同义的
时间差又是被叫做时长，这两种叫法也是同义的
时段通常没有另外的叫法，但很多时候会直接被称为时间差或者时长，在不会对问题思考造成严重错误的条件下，我们默认这种称呼是合适的，但从严格意义上来说这种叫法是错的，尤其在相对论问题中


时间的测量定义（也叫物理定义）：
要定义时间的几个概念，先要定义 钟 的概念：
假定可以找到某种可以自发重复发生的物理变化过程，该种过程满足条件：
1----每一次该种物理变化都能够找到明确的变化起点事件和变化终点事件
2----同一次该种物理变化的变化起点事件和变化终点事件之间有持续性
3----每一次该种物理变化的变化起点与其前一次该种物理变化的变化终点间没有持续性（或称之为在时序上重合）
4----不同次的该种物理变化所对应的连续性都相同
5----该物理变化是不可逆的
则可以认为我们找到的这种能自发重复发生的物理变化具有”周期性“或”均匀性“
满足这种要求的可自行重复发生的物理变化过程，即可被视为一个”钟表（简称钟）“过程
下面我们定义时间的三个具体概念：

时刻：
钟过程的每一次重复发生的起点事件就是上一次过程的结束事件，因此我们把每一次钟过程的起点事件用实数来标定为一个时刻，并用实数的大小关系来表示各次钟过程的起点之间的时序先后关系
通常我们认为时刻不具有持续性，因为它所对应的钟过程的起点事件是被视为没有持续性的，因此才可以在数学上对应于一个确定实数单值

时间差：
时序靠后的时刻值减去时序靠前的时刻值得到的数学差值
在很多情况下，所谓时序靠后指的是时刻对应的实数值较大，很多时候而并不是真的考虑具体时序关系，因为不同参照系的时刻之间不一定能很轻易确定时序先后，而同一观察者在不同地点测量的两个时刻之间未必描述同一个物理过程，但是物理学中仍然要求尽可能地在确定了时序先后顺序之后才去做差

时段：
同一观察者在同一地点测量的两个时刻，按照时间差定义相减得到的数学差值

【空间】
古典释义：容纳物质存在的范围称为空间


这个古典释义并不能够在物理中准确应用，因为我们目前尚不清楚某些物质属性确实是独立的物质属性，还是我们观测<高维空间结构在我们三维空间中的投影>时获得的观测效应
直白一些来说，我们不知道是否真的存在更高维的空间结构，所以空间这个词是否仅限于指代三维空间，还是一个有争议的问题
但在现代理论物理学中，物理学家倾向于认为高维空间结构存在，而很多物理属性实际上是我们观测<高维空间结构在我们三维空间中的投影>时获得的观测效应，因此在诸如弦论之类的物理学专著中，空间一词可以涵盖超过三维空间的领域


尽管空间这个概念并不是一个准确的概念，但并不影响我们用测量手段给出与之相关的一系列物理概念的准确定义：


【尺】
在讨论时间的时候，我们定义了时间测量工具”钟“的概念，在这里的”尺“显然是空间测量工具的概念（之一）
首先，尺也具有确定方向性
在数学上，连续曲线（一维）通常指光滑连续的曲线，我们可以对曲线规定出它的自然坐标系：
即给曲线上每一点指定一个实数值，并要求所有点的实数标度（坐标）应该是按照实数大小顺序递增排列，形成曲线上的自然坐标系，并以此给出曲线的坐标递增方向
尺上的方向概念类似曲线上方向的定义，尺也具有类似曲线的自然坐标系，所以尺上也有坐标


其次，尺也具有容纳的属性

容纳属性通常在理论意义上被称之为”连续性对坐标变量可求导“。这个解释起来稍微有点麻烦：
数学上的连续曲线，并不都指光滑连续曲线（一维），还有分形曲线（非一维曲线，例如某些看似噪波的具有无穷精细结构的曲线）的存在，分形曲线也属于连续曲线
但是光滑连续曲线的连续性（这里我们还没有给出长度的概念，所以还得说连续性，其实这里隐含了长度概念）在数学上是能够对坐标求导数的（准确说是长度能对坐标求导）
而分形曲线则不一定都能满足：其连续性（长度）能对任意一点坐标求导，甚至它们的长度定义也不那么简单
因此我们要求我们的尺必须是一维连续曲线型的，即”连续性对坐标变量可求导“的
其实当我们在后面介绍了长度定义之后，各位会更直观地明白：
要求尺能够满足”连续性对坐标变量可求导“，其实就是为了能在尺上定义长度
当我们的尺满足了”连续性对坐标变量可求导“这个要求，我们可以对尺取任意两段，即找至少个4坐标点a,b,c,d（我们假定三点坐标递增a<b<c<d），它们沿着尺的坐标增大方向可以形成两个坐标差b-a和d-c（大值的坐标减去小值的坐标）
当我们把b-a平移到d-c的位置去，我们的尺应该满足如下条件：
如果在数学上b-a=d-c
那么我们在尺上所做的平移应该导致原来的a点移动到c点，即a和c重合；且同时有另一结果：
原来的b点移动到d点，即b和d重合
简单来说就是数学上相等的差值对应尺上坐标之间的尺的部分的空间容积相等
我们要求对任意坐标a<b<c<d，在b-a=d-c时，我们的尺都一定满足平移b-a到d-c之后，a和c重合，且b和d重合
这样的一件一维测量工具，就叫 尺，它满足”标量平移不变性（就是我们上面要求的平移后一维容积相等）“


最后要说的是，别忘了尺可能有形状，我们也没有定义一定必须是直尺（这个观点在相对论这类非欧几何时空理论中尤为重要），尺对应的曲线也可能会与自身相交（形成某种循环结构），原则上来说，上面对于尺的定义有一定通用性，当然在具体问题中可能还要有修正（我们在这里就不涉及修正的问题了），但我们要清楚的是，上述定义暗含了一个条件：
尺可以在平移过程中改变形状，以保证尺上的点与被测一维空间部分的端点重合
我们的尺能够在任意变形的情况下依旧满足”标量平移不变性“，这是尺的实质特征


【长度】
长度一词专指空间长度，而在时间概念中有时长的说法，长度是物理学上对于一维空间部分的容量的描述，而实际上它也暗含了空间连续性（这个是通过尺的数学可导性暗含的，我们不重复说了）
在我们上述定义的尺的概念之下，如果我们用平移这把尺，使被测量的一维空间部分的至少2个端点与尺上两点分别重合（注意我们的尺可以任意变形来适应被测一维空间部分的形状），那么尺上这两点的坐标（每点一个，共计两个坐标）就可以按照其坐标值，大值坐标减去小值坐标得到一个数学差值，这个差值一定不是负数，它称为长度


由于尺实际上是可以任意变形的，所以我们所说的长度当然包括直线和曲线长度

【角度】

通常我们这里指的是二维空间的角度，但很多时候它也会被扩展到三维空间中去使用，比如数学中的空间曲线夹角或者曲面夹角（实质上都是二维空间的角度）
定义这个概念之前，我们有必要谈一谈二维空间（我们不涉及更高维数，而且我们要提醒大家的是，我们下面的讨论最多能够适用到三维空间，四维空间或更高维空间，已经不能凭直观来想象）


一个二维空间，数学上的抽象定义是空间中每一个容量为0的结构（我们不直接说是点，因为可能导致其他问题，例如点的邻域的连续性问题，我们不想讨论那么多太复杂的与本部分主题无关的东西），可以用两个坐标来定位


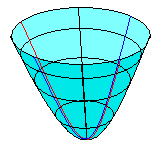
例如图中曲面上任意一点可以用经向坐标（通过该点的抛物线上的自然坐标系中的坐标）和纬向坐标（通过该点的圆线上的自然坐标系中的坐标）这两个坐标来定位

但是我们很容易想到一个问题，经纬向的自然坐标系都是一维坐标系，它们要组成一个二维坐标系，必然要有一套组成规则
如果你想到了这个问题，那么就表明你触及到我们问题的核心了：
一个二维结构绝不是一系列一维结构的随意组合，二维结构之所以不再是一维结构，就是因为它上面存在了新的空间结构规则
所以我们讨论二维空间中的位置关系的时候，不仅要讨论长度（距离），通常还要讨论角度，因为角度是用来描述一维空间结构如何组成二维空间结构的规则用到的概念


物理学中的二维角度定义，与几何中二维角度定义一致，当两条曲线相交时，我们取它们交点附近的两条曲线的尽可能小部分（都要包括交点在内），将所取的两部分（每条曲线取一部分）近似看作直线，这样确定了一个非常微小的平面结构，在这个平面结构中去根据根据平直空间结构下定义的角度概念来定义两条直线之间的夹角


所以最终我们还是要定义平直空间中的两直线夹角


说到平直空间，很多人认为首先是一维平直空间的概念，即直线的概念，实际上我们并不能孤立定义一条直线，因为直这个概念本身由角度来定义，在我们没有定义角度前，扯直线的概念就等于是循环定义（角度由直线定义，直线又由角度定义，实际上两者都是架空的定义）
所以我们首先讨论的是面结构（未必是平面，因为你还没定义角度，平面的平也是靠角度定义的，但是曲面不需要依靠角度来定义，所以说曲面更具有一般性）
我们还要强调的是我们这里谈论的曲面都是光滑曲面，它不仅由光滑曲线构成，而且所有构成它的光滑曲线之间的组织方式也是光滑的（这不是数学语言，数学语言会涉及到各种可导性，还会考虑到那些分形曲线和分型面结构，那对我们来说太复杂，而且和本主题没多大关系，所以我们用一种不太专业但比较直观的说法来描述这个问题）
当我们随意取曲面上任意小的一个部分，这个小曲面内肯定包含了两条小的相交曲线，它们只有一个交点（如果不止一个，那说明我们取的小曲面还不够微小，还要更小，直到只剩下一个交点）
在这种条件下，我们要求所取的”小曲面“满足：
所有通过这两条小曲线的那个交点的小曲线之间都不再有另外的交点
通过这个共同交点的所有小曲线形成一个曲线族，我们将它们称为经向曲线族，我们可以将它们共同的交点定义为原点，其经向坐标为0，即所有小曲线上的一维自然坐标系都把这一点作为0坐标点重新规划坐标系，而且我们知道原点把每一条经向曲线分为两部分，一部分的坐标沿着曲线正向增大，一部分的坐标沿着曲线负向减小

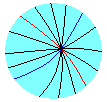
把一个我们选好的小曲面部分放大后的样子，红线和蓝线为我们最先选取的那两条线，黑线是和它们通过同一交点的曲线族（的几个代表成员）



然后我们以那个交点为中心，画一个任意的圈（形状可以不规则，但仍然必须是光滑曲线，既然说它是圈，那就必须是条封闭曲线），并保证它绝对不通过那个交点：

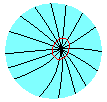
类似地我们还可以画更多的圈，并且加一条要求：
所有的圈之间都没有交点

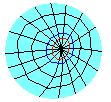
假定我们画了无数个圈，它们可以称之为同心圈族，也是一个曲线族，我们把它们称为纬向曲线族，然后我们给出一个新规定来调整纬向曲线族：
同一条纬向曲线圈与所有经向曲线有且只有一个交点，这一系列交点与经向曲线族的原点（也就是纬向曲线族的共同的中心）之间的长度都相等（请注意这里用到了前面说的曲线长度的概念）


这样我们重新做一些规定：
1-----同一条纬向曲线圈上所有的点的纬向坐标（红）都相等
2-----同一条经向曲线上所有的点的经向坐标（蓝）都相等
最后就是这个样子：

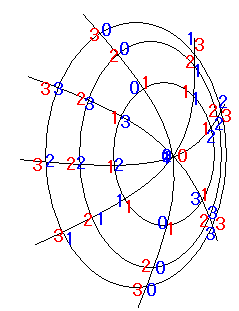
原点的经向坐标是任意的，但纬向坐标是0（确定的）
这个类似我们地球仪上的经纬网络，经纬网络就是用经纬两个曲线族来规划球面的二维坐标系，只不过坐标的数值设定和我们这里不同


【注】别看我图中画的纬线圈全是椭圆，实际上可能是不规则的光滑封闭曲线形状，别忘了我们是在曲面上说事，我们的曲面可能各种凹凸不平，我画成椭圆只是为了画着省事

另外，原则上来说，当我们选取的小曲面足够小时，它已经近似为平面了，但是我们为了让大家时刻记得我们是在曲面上说事，所以我画的还是曲面（有些夸张）

现在我们要定义 类似平移 和 局域平面 的概念：
当我们在之前取的那个小曲面上建立了一个经纬坐标系之后，我们尝试在这个小曲面上移动这个经纬坐标系，即保持它的面结构（我们之前总结的两条规定）关系不变来移动整个经纬坐标系
移动后的小曲面上新旧坐标系位置我们用不同颜色标出（红新蓝旧）：

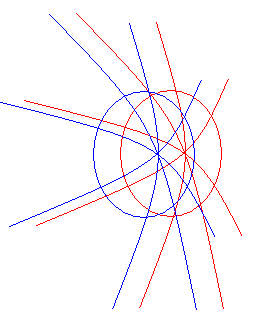如果我们所作的移动能够保证任意同一条经向曲线（纬向曲线我们不在乎）在新旧坐标系位置上的两个”分身“没有任何交点（在我们的小区面区域内），我们称这个移动叫 类似平移（物理中的平移都是类似平移，而不是数学中严格定义的平移）
如果我们把旧坐标系移动到小曲面内任意的位置时，都能找到至少一种 类似平移 的移动方式使新旧坐标系中同一经向曲线的两个分身没有任何交点（但不表示所有新坐标系中的同一条曲线的诸多分身之间没有交点，因为有时候为了达到无交点的目的我们会对坐标系进行转动，当然我们现在没有定义角度，还不能用到转动这个概念，但是你心里可以大概有数，转动的情况可能存在），我们称这个小曲面是个局域平面


实际上在物理中，我们通常谈到的平面，都是局域平面，我们不需要去研究数学中严格定义的真正的平面，局域平面对物理中的空间问题来说已经足够用了


我们之所以要谈经纬坐标系和类似平移、局域平面这些概念，是因为我们的主题”角度“需要这些概念来支撑，现在万事俱备，我们进入正题：


假定现在有两条相交曲线（注意不是我们前面说的微小曲线，是真正的大曲线）：

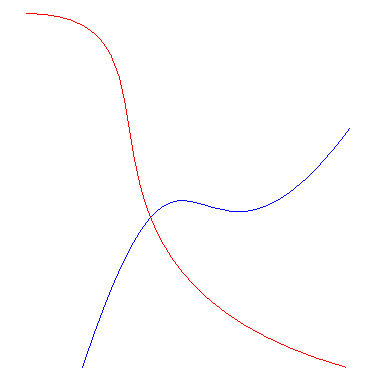它们有一个交点，我们想要知道交点附近的平面空间结构的情况，并以此来描述两条曲线之间的位置关系（实际上是定义夹角）
那么我们在交点处选择一个尽可能小的小曲面，我们可以无限缩小选取范围，使得选取的小曲面无限近似是一个局域平面（移动它内部一个任意的经纬坐标系到它内部任意位置，新旧坐标系中同一条经线都没有任何交点），并且我们以那个交点为原点建立一个经纬坐标系（要包括这两条曲线在小区面内的部分也作为经线）

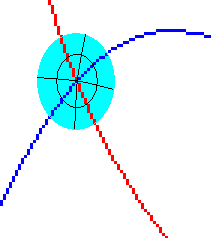我们定义：由原点某一侧红线为起始，其经向坐标为0，任找一条纬线圈，与该经线相交的点为起点（其经坐标当然是0），令纬线圈总长度为2π来标定纬线圈的一维纬向坐标系（经坐标系），按图中方向（逆时针）令经坐标递增

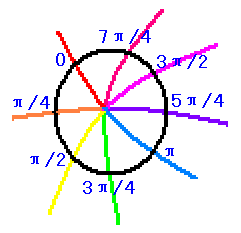过这条纬线圈上任意一点都一定有且只有一条经线，该经线的经坐标就是纬线圈的自然坐标系中该交点的坐标
实际上纬线上有无数点对应于0~2π之间的所有实数坐标，因此就可以有无数条经线分别于每一点处于纬线相交
则我们可以得出，按照逆时针方向来看，经线的经坐标在递增，直到回到0经线为止（0经线即2π经线）


由此我们可以在经纬坐标系中找到最初蓝线对应的经坐标9π/16：

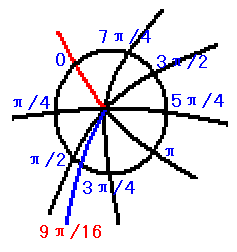实际上，由于蓝线是曲线，而且当我们选取不同大小的纬线圈时，会与蓝线有不同交点，按同样规则来定义经纬坐标，小的纬线圈与蓝线交点对应的经坐标可能与大的纬线圈不同

数学上通常规定：当选取的纬线圈越来越小不断趋近于经纬坐标系原点时，按照上述方法给蓝线找到的一个经坐标，在数学上会有一个极限值，这个极限值叫做”红线到蓝线的转角“
它就是我们常说的两条曲线之间的夹角的概念（与数学上用直线定义的夹角概念等价，但我们介绍的这种定义方法可以回避掉直线、平面等概念，因为我们不想花篇幅定义这些无关的概念）
【注】经纬坐标系的定义过程其实类似于我们建立一个量角器你懂的

题外话：
我们为什么要说类似平移，而不直接说平移，因为我们在曲面内移动坐标系，意味着坐标系不能跑到曲面以外的三维空间去，换而言之，被移动的坐标系是会自动变形适应曲面的，只是保持坐标系的那两条规定不变，因此，这种移动可能不是真正的平移（保持坐标系各部分形状不变）
而满足局域平面要求的小曲面也未必就是真的平面，比如说我们可以把一张世界地图上的南极部分绘制在一个平面上，也可以绘制在球面上，都不影响地图的经纬坐标系结构，而我们很清楚这个地图显然允许我们随意移动经纬坐标系，保证经纬坐标系中同一条经线的新旧位置残影之间”平行“，这个结论我们可以轻易从平面上绘制的南极地图看出，它也同样在球面南极地图内成立
因此事实上我们单凭这种平移限定是无法绝对确定一张曲面是否是平面的


因此很多时候我们会怀疑，我们的三维世界是不是真正的平直三维空间，是否只是某种类似平直的三维空间，实际上只是更高维空间的一部分？
这个问题目前尚无答案，因为从整个宇宙的角度来看，我们周围的空间就相当于一个局域的平直空间，它只能反映它附近的空间特性，而不能反映广大空间的整体性质


所以我们说物理学中的平移都是指类似平移，而物理学中的平面都是指局域平面
类似地，直线也只是局域直线，三维立体也只是局域的平直立体空间


局域性是物理学中一个很深刻的主题，我们这里只是稍带提到它，说实话这只是冰山一角

待续

【物体长度】
提到物体的长度，我们回顾一下前述的空间长度（距离）的概念：
在空间长度（距离）概念中，我们定义的尺是会适应空间本身的弯曲形状而变形的，例如一维尺可以在测量一维空间容量时，随着一维空间（一维曲线）的形状弯曲，因为尺就在这个空间内
但是当我们用尺去测量空间内的其他物体的时候，这就不是测量空间本身的容量了，尺是不会适应被测量物体的形状而变形的，因为尺独立于被测物体之外


例如我们测量一条曲线段的长度，我们定义这条曲线段的长度是当我们把它拉直之后，用直尺去测量它两端坐标之间的坐标差得到的长度，尺不会改变自身去适应曲线段，而曲线段要做形变（哪怕只是理论上想象的形变，即用相关数学手段去获取它被拉直的效果，参见微积分学中的曲线长公式）


我们这里不会给出曲线长公式，我们只说说为什么一个弯曲的曲线比直线要长，顺便说说这个定理为什么并不绝对成立


我们还是要具体说物体长度的测量，即我们是怎样把一个弯曲物体拉直的
当我们默认测量者所在的空间为平直空间时，我们可以用勾股定理来很方便地说明曲线为何比直线长：

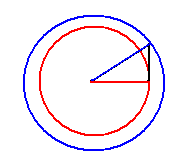图中的红横线对应红圆的半径，蓝斜线对应蓝圆的半径，我们知道圆越大对应它的半径越长，所以蓝线必然比红线长
而之所以如此，是因为根据蓝线长度公式：
蓝线长度=√（红线长²+黑线长²）
虽然黑线并不在蓝线方向上，但黑色竖线对蓝线长度有正值贡献


而我们随便看一条曲线，它可以近似为折线：

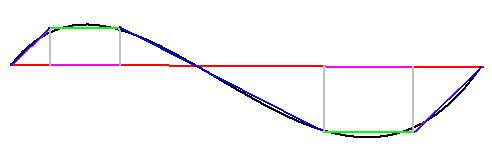绿线和粉线的长度都是一样的，但蓝线都比对应的红线多了灰线的贡献（类似前面勾股定理的例子），所以蓝线都比红线长，因此折线总长比横直线要长，我们看到曲线的长度和折线很接近，因此可以很容易看出曲线要比横直线长


在数学分支---解析几何中，只要将曲线分割成做够多的足够小的部分，就可以把这些小部分近似成小折线（或者说是曲线各点处的一个微小的切线段），用曲线函数分别计算它们的斜率（即小折线位置处曲线函数对横坐标的导数，对应于小斜线横纵长度分量之间的比值），就能用勾股定理计算每一小段的长度，然后把所有微小的斜线长度相加得到整条曲线的长度，这是一个积分（积分就是对无数个微小单元的值求和，它相当于一个求和运算，只不过它的加数是无穷多个，所以它是个数学极限）


我们上面一段话其实已经给出了曲线长公式的推导思路，不过我们不想就这个话题说更多，有兴趣的朋友可以自己去查资料






当一个物理问题摆在我们面前时，我们如何去判断它要研究的是空间长度（距离）还是物体长度呢？
正如我们前面说的，当测量者本身处于被测物限定之下，例如我们被空间所容纳，我们的尺也被空间所限制，这时我们的尺如果以空间本身的两点间部分作为测量对象，那就是测量距离，尺要随着空间本身的弯曲形态变形
如果被测物体并不能影响观察者和他所用的尺，那么这时测量的就是物体的长度，尺还是随着空间本身的弯曲形态变形，而并不随着被测物体的弯曲形状变形
在经典力学中，这个区分并不重要，因为经典力学认定空间是平直的
在相对论中则认为空间会发生弯曲（有时间分量上的贡献），因此做上述概念区分尤其显得重要

【位矢（位置矢量）】
物理学中研究时间时通常忽略时间的方向，把时间视为一个标量（只有大小），因为我们默认时间的方向是单一不可逆的（这个目前为止还没有发现反例）
物理学中的 位置 这一概念，则通常是个矢量（有大小又有方向的量），因为物理问题中空间方向至少为两个（一维情况下），方向这个因素不能省略
举一个最直观的例子：
已知有一条走廊，维德的房门在走廊正中间，维德现在站在走廊中，他的位置就可以用一个矢量表示，即从维德的房门指向维德的一个矢量（方向），大小是房门到维德的长度（距离）
如果我们考虑更复杂的情况，例如地球上的一个卫星监测站正在监控绕地轴飞行的某一处于赤道平面上的卫星，那么卫星的位置就是：

从监测站指向卫星的一个矢量，大小是此时监测站到卫星的距离，很方便吧


位矢的概念的最大优点并不只是用起来方便
我们看下图：对于相同的一个位矢来说，无论我们以它的起点为原点规定何种坐标系统，这个位矢本身永远是不变的，因此在物理中只要用位矢来确定位置，就可以在研究问题时完全不考虑坐标系环境，这会大大简化问题的处理

因此，在物理学（尤其是理论物理）中，只要谈到 位置 这个概念，通常说的就是位矢（位置矢量）
另外，矢量具有一个特点，它满足平移不变性，即对这个矢量进行任意平移操作，矢量的大小和方向都不变（也就是矢量不变）
因此在研究物理问题时，可以通过平移矢量很方便地比较两个矢量之间的大小关系和方向关系，位矢同样可以用这种手段进行比较

【轨迹方程（轨道方程）】
试想把一个运动物体在每一时刻的位置点都画在同一张图中，一定可以形成一条运动曲线，物理学上把这条曲线叫做运动物体的轨迹
当我们以观察者为中心建立了一个坐标系，那么运动物体的这条“轨迹”中的每一点都可以在这个坐标系内定位（用位矢 或者 用坐标）
如果我们把轨迹中的每一点P的位置r与它对应的时刻t（请注意，物理书中有时会写作“时间”，但你应该清楚“时间”在这里专指时刻，而非其他时间概念）相对应，形成一个函数：
r(t)
这个函数叫做位置函数，表示点P的位置r随着时刻t的变化而变化
当这个函数满足某种数学条件P时，可以写成方程形式：
r(t)=P
这里条件P可以是常数或者函数（请注意：r(t)=P形式通常叫做 解形式，不是所有轨迹方程都一定要写成解形式，相反地，绝大多数条件下轨迹方程都写成非显式形式，即其中根本不含有位置r这个变量，而是含有诸如坐标x,y,z等变量的形式）
那么这个方程r(t)=P叫做物体的轨迹方程（轨道方程）


当我们用位置矢量r↑表示位置r时，该方程就变成r↑(t)=P，称为位矢轨迹方程
当我们用坐标(x,y,z)等（还可以有其他类型坐标系下的坐标，例如球坐标或者柱坐标）表示位置r时，该方程就变成r(x,y,z)=P


例如一个匀速圆周运动的具体例子：

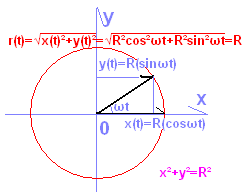红色为轨迹方程（满足条件是位置矢量的大小恒等于圆周半径R），它是解形式的轨迹方程


蓝色为轨迹方程的参数方程形式，即分别表示出了直角坐标系下横纵坐标的方程并联立成方程组，时间t为参数
粉色为消掉参数以后的轨迹方程
蓝色和粉色这两种非显式（不明显含有位置r）的形式才是最常见的轨迹方程形式